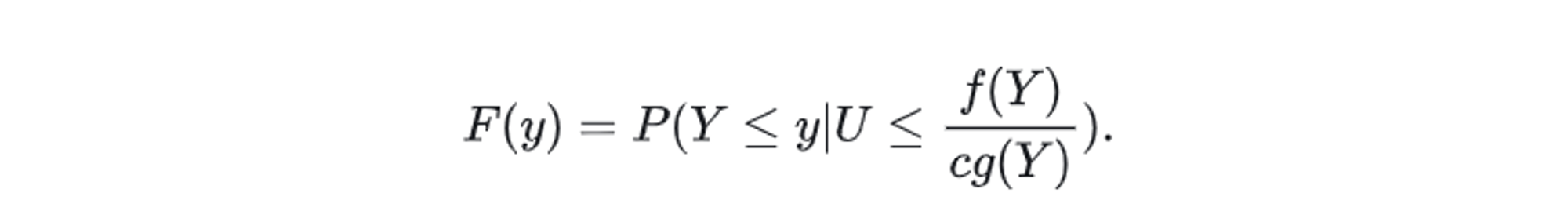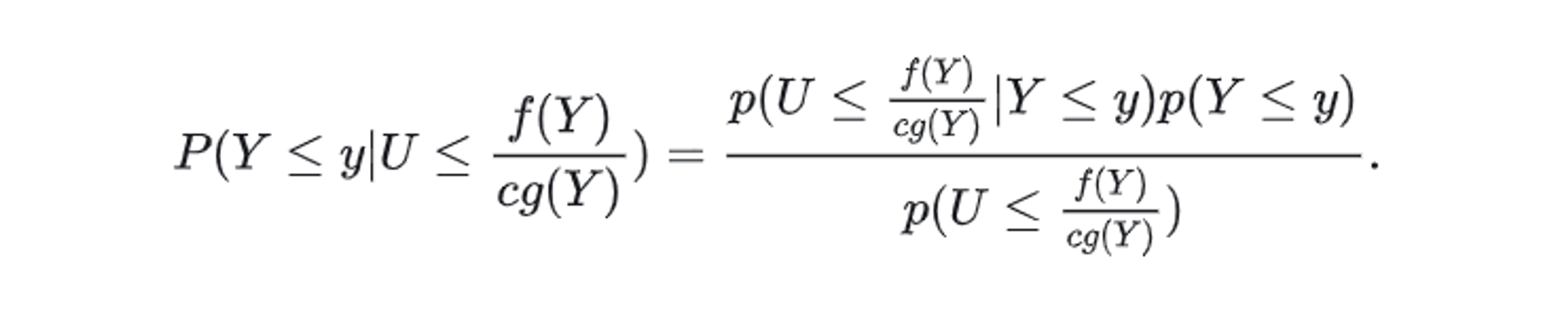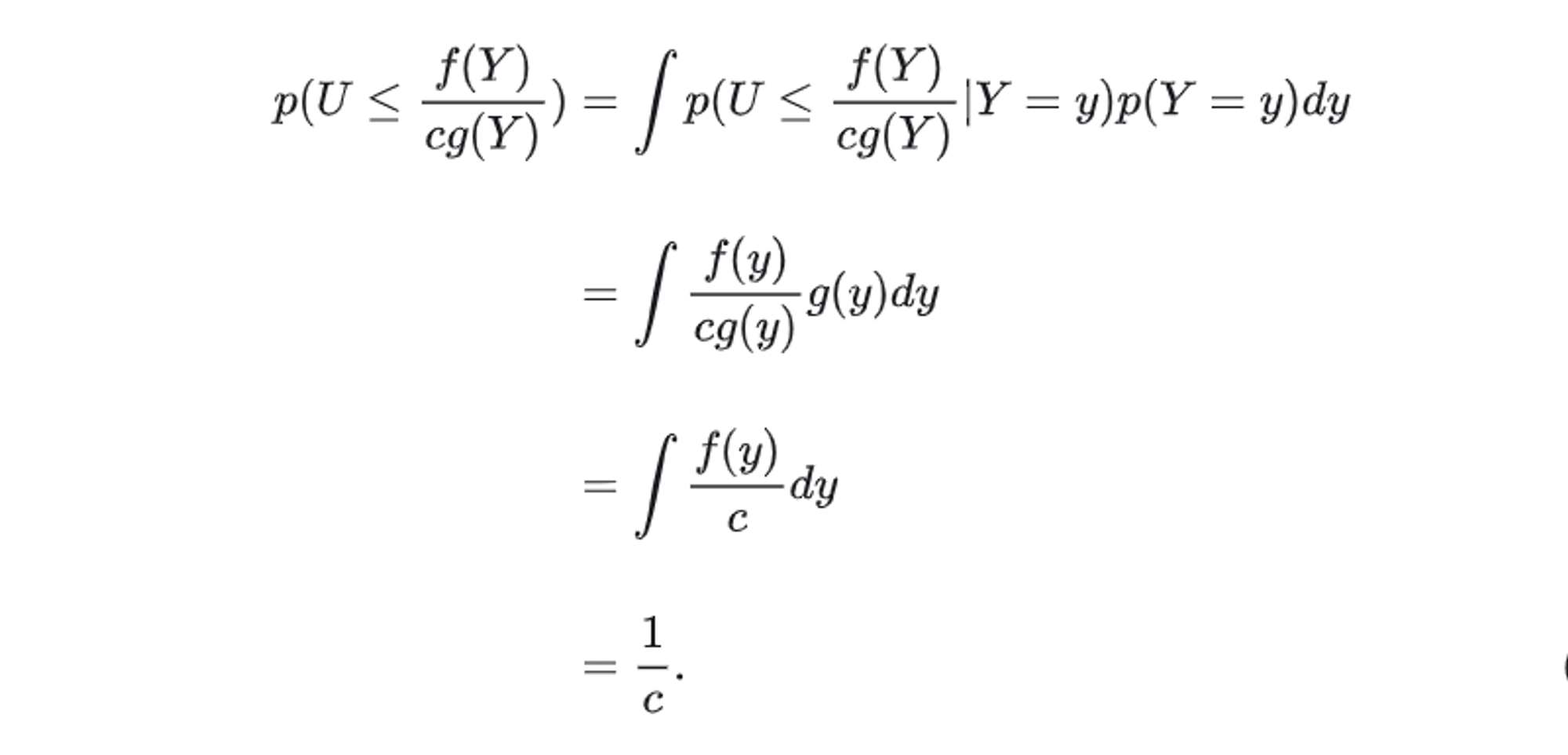Sampling Method
0. 前言
比如在老虎机场景, 我们想知道哪一台老虎机的赢面更大, 通常是给定所有老虎机 “赢” 的参数分布 , 比如 Dirichlet distribution, 初始化 $\alpha1 \ \alpha2 \ …$ , 然后根据实际数据采样, 更新 Dirichlet distribution 的参数即可.
具体采样流程(通常使用在类似多臂老虎机场景) :
[1] 首先假设 参数p的先验分布 (比如 beta 分布 $B(m, n)$, Dirichlet 分布 $D(a, b, c, …, z)$)
[2] 然后 基于该分布 , 采样一组参数(就是各个机器的成功概率) , 然后基于当前的参数抽卡, 并选择最大的p对应的老虎机作为成功case , 然后观察其结果, 并更新对应参数(比如实际是另外一个老虎机赢了). 重复此步骤.
这里就会涉及到一个问题, 对参数采样, 怎么采才能尽可能的符合、或者接近参数本身的分布?
1. 基于Monte-Carlo的方法
- 引理1
设 X 是一个随机变量,其分布函数$f(x)$, 累积分布函数 (CDF, Cumulative distribution function) 为 F(x) , 该函数是一个单调递增的函数, 其值域为[ 0 , 1 ]. 现在定义一个新的随机变量$Y = F(X) $ , 则 随机变量 $Y$ 的分布是均匀分布.
- 证明
对于任意实数$y$ , 我们有:
\[P(Y<=y) = P(F(X) <= y) = P(X <= F^{-1}(y) = F( F^{-1}(y))\]由于F(x)是单调递增函数, 因此$F^{-1}(y)$具有唯一解 $x$ , 令$x = F^{-1}(y)$ , 则有 $F(x) = y$ .
因此
\[P( Y <= y) = F(F^{-1}(y)) = F(x) = y\]即有
\[P( Y <= y) = y\]即 Y是均匀分布
1.1 逆变换采样法
设 X 是一个随机变量,其分布函数$f(x)$, 累积分布函数 (CDF, Cumulative distribution function) 为 F(x). 则依据如下采样过程, 得到的x是服从分布$f(x)$的.
- 从均匀分布 U(0, 1) 中生成一个随机数 u
- 计算 F(x) = u 的解 x
- 输出 x 作为采样结果
- 证明
根据引理1容易知道, 如果从均匀分布 $U(0, 1) $ 中生成一个随机数 u,并令 $x = F^{-1} (u)$,则 $x$ 服从原分布$ F(x)$。(理解为本身这个$F$就是我们想采样的 $f$ 对应的 $F$, 那反函数求解出来的 $x$ 自然就是 满足 $f(x)$ 和 $F(x)$ ) , 即为 逆变换方法 , 几个具体实现: https://lwz322.github.io/2019/06/02/ITM.html
1.2 拒绝采样法
- 准备工作
- 已知 概率密度函数$f(y)$, 我们需要依据这个分布进行抽样
- 找一个任意能够直接进行采样的分布$g(y)$ (比如均匀分布)
- 找一个常数 $c$, 满足对 $\forall y$ , 均有 $c \times g(y) >= f(y)$, 即 $c$ 是函数 $\frac {f(y)} {g(y)}$ 的上界 或者 $c \times g(y)$ 能够覆盖 $f(y)$
- 抽样流程
- 从 $g(y)$ 中中随机采样一个样本 $y_i$
- 从均匀分布 $U(0, 1)$ 中采样一个随机数 $u_i$
- 如果 $u_i <= \frac {f(y_i)} {c * g(y_i)}$ 成立, 则保留该样本 $y_i$, 否则返回 step1重复. 可以证明, 这样从 $g(y)$ 抽出的样本 $y_i$ 是满足概率密度函数 $f(y)$ 及其对应的CDF函数
- 证明
证明上述采样方法生成的样本服从 $f(y)$ , 等价于证明以下内容
其中 , U 为 $[0 , 1]$ 的随机数, $y$ 是从 $g(y)$ 采样得到的 , $F$ 和 $G$ 分别是 $f$ 和 $g$ 对应的累积分布函数.
根据贝叶斯公式
\[P(A|B) = \frac {P(B|A)P(A)} {P(B)}\]将 $P(Y<=y \mid U <= \frac {f(Y)} {c * g(Y)})$ 用贝叶斯公式转化为:
现在分别来看 右边的 3个式子
(1) 分母
\[P(U <= \frac {f(Y)} {c*g(Y)}) = \int P(U <= \frac {f(Y)} {c*g(Y)}| Y = y)p( Y = y)\]由于 y 是从 g 中抽样得到的 , 那么 $p( Y = y) = g(y)$ , 不妨假设此时 y 的抽样结果 : $Y = y$ , 又因为 U 是均匀的 0 , 1 分布 , 按定义 我们有
\[P(U <= \frac {f(Y)} {c*g(Y)}| Y = y) = \frac {f(y)} {c*g(y)}\]此外, 由于$\int f(y)=1$ , 我们有
(2) 分子 $p( Y <= y)$
按照定义
\[p( Y <= y) = G(y)\](3) 分子 $P(U <= \frac {f(Y)} {c*g(Y)} \ Y <= y)$
\[\begin{align*} P(U <= \frac {f(Y)} {c*g(Y)} \mid Y <= y) &= \frac {P(U <= \frac {f(Y)} {c*g(Y)}, Y <= y)} {P(Y <= y)} \\&= \frac { \int_{-\infty}^{y} P(U <= \frac {f(w)} {c*g(w)} , Y = w <= y)\ dw}{G(y)} \\ &= \frac { \int_{-\infty}^{y} \frac {f(w)} {c*g(w)} *g(w) \ dw}{G(y)} \\ &= \frac { \frac {F(y)} {c*G(y)} * G(y) }{G(y)} \\ &= \frac {F(y)} {c*G(y)} \end{align*}\]于是, 原始公式可进行转化, 从而证明完毕:
\[P\big(Y<=y | U <= \frac {f(Y)} {c*g(Y)}\big) = \frac { \frac {F(y)} {c*G(y)} * G(y) } {\frac {1} { c }} \\ = F(y)\]
- 直觉理解
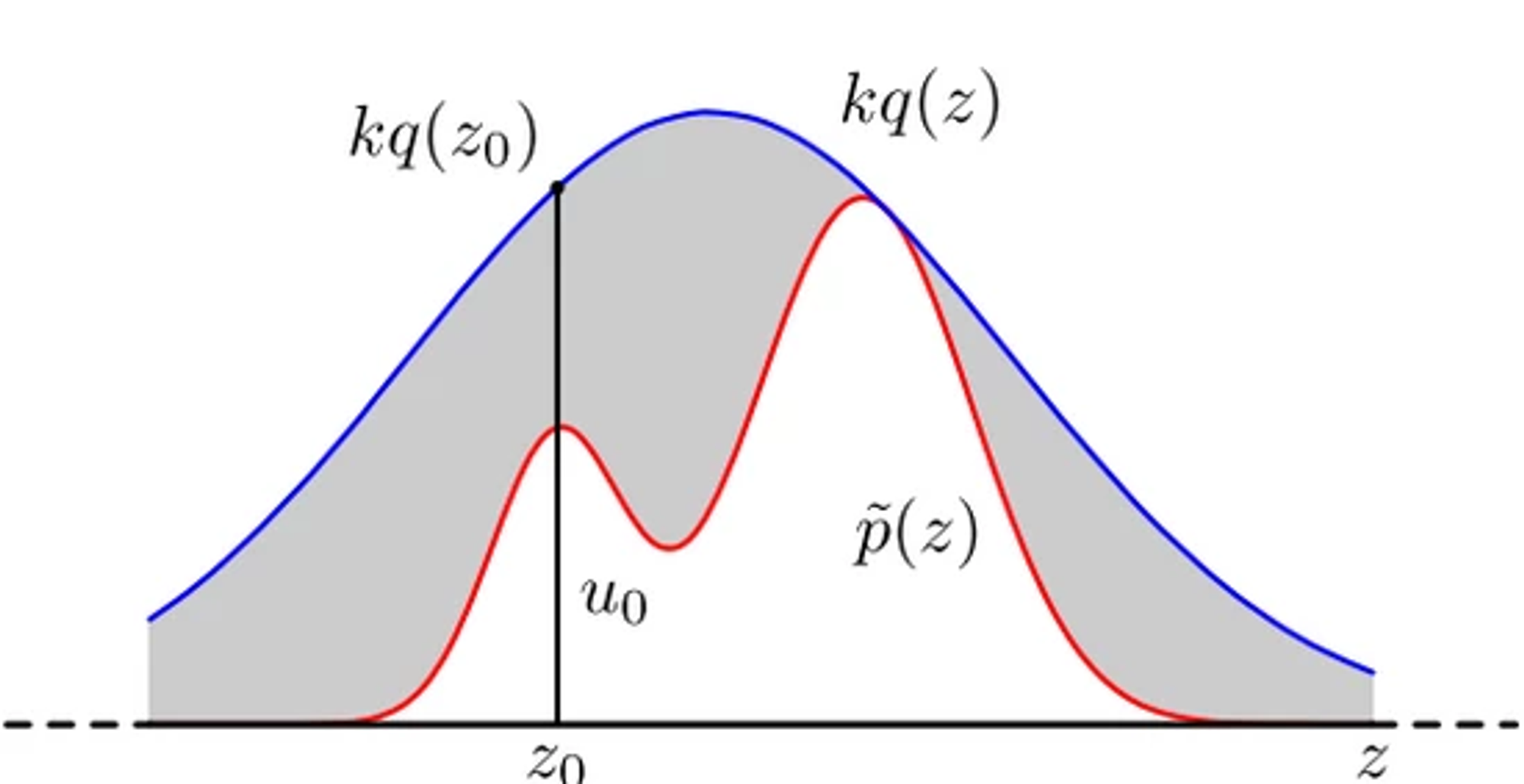
假设复杂分布 $P(z)$ , 存在常数 $k$ 与 任意分布 $q(z)$ , 以 $z_0$ 点为例, 画直线, 任意从均匀分布抽取一个点 $u_i$, 可以理解为在 $x = z_0$ 这条直线上取一点: 就是 $u_i * k * q(z_0)$, 其处于阴影即拒绝 (即 $U * k * q(z_0) > p(z_0)$) , 处于白色区域即接受( $U * k * q(z_0) <= p(z_0)$ ) , 这样从 $z_0$ 出来的点对应的最大概率就是$ f(z_0) $ , 等价于是从 $f(x)$ 抽样出来的
上述2个方法都属于Monte-Carlo 方法, 并且是已知 $P(\theta)$ 的情况下 , 然后在某些特殊场景下, 已知了 参数的后验分布 和 先验分布 的关系(比如之前提到的共轭) , 才能得到一个比较简易的形式 , 直接对后验分布更新. (当我们面临无法得到具体形式的非共轭后验分布时,我们无法采用这种算法。)
然而, 面对一些复杂的分布, 即使我们已知了 $P(\theta)$ , 再利用贝叶斯公式的时候 , 其分母涉及到积分, 往往也是很难求解的
\[P(\theta|X) = \frac {P(X|\theta)P(\theta)} {\int P(X|\theta)P(\theta) d \theta}\]上述提到分母有时候很难进行积分,对于这个问题,一个直观的想法就是 ,能不能通过某个手段把 分母去掉?
\[P(\theta_a|X) = \frac {P(X|\theta_a)P(\theta_a)} {P(X)}\] \[P(\theta_b|X) = \frac {P(X|\theta_b)P(\theta_b)} {P(X)}\]二者做比值
\[\gamma = \frac {P(\theta_a|X)}{P(\theta_b|X)} = \frac {P(X|\theta_a)P(\theta_a)}{P(X|\theta_b)P(\theta_b)}\]这样避免了分母的积分,这里 $P(\theta_a)$ 可以参考 Dirichlet Distribution (多维)或者 Beta Distribution (二维). 思想是这样的, 不过需要一点点其他知识.
未完待续…