Probability Calibration

0. 前言

在分类的时候, 我们不仅希望预测类别, 还希望输出概率, 但是有些模型是不能直接输出概率的, 或者输出的概率只是一个相对的, 这时就需要校准

一个良好的、校准过的分类器, 输出的 prob=0.8, 就是可以理解为当前样本有80%的概率是正样本

1. 校准曲线

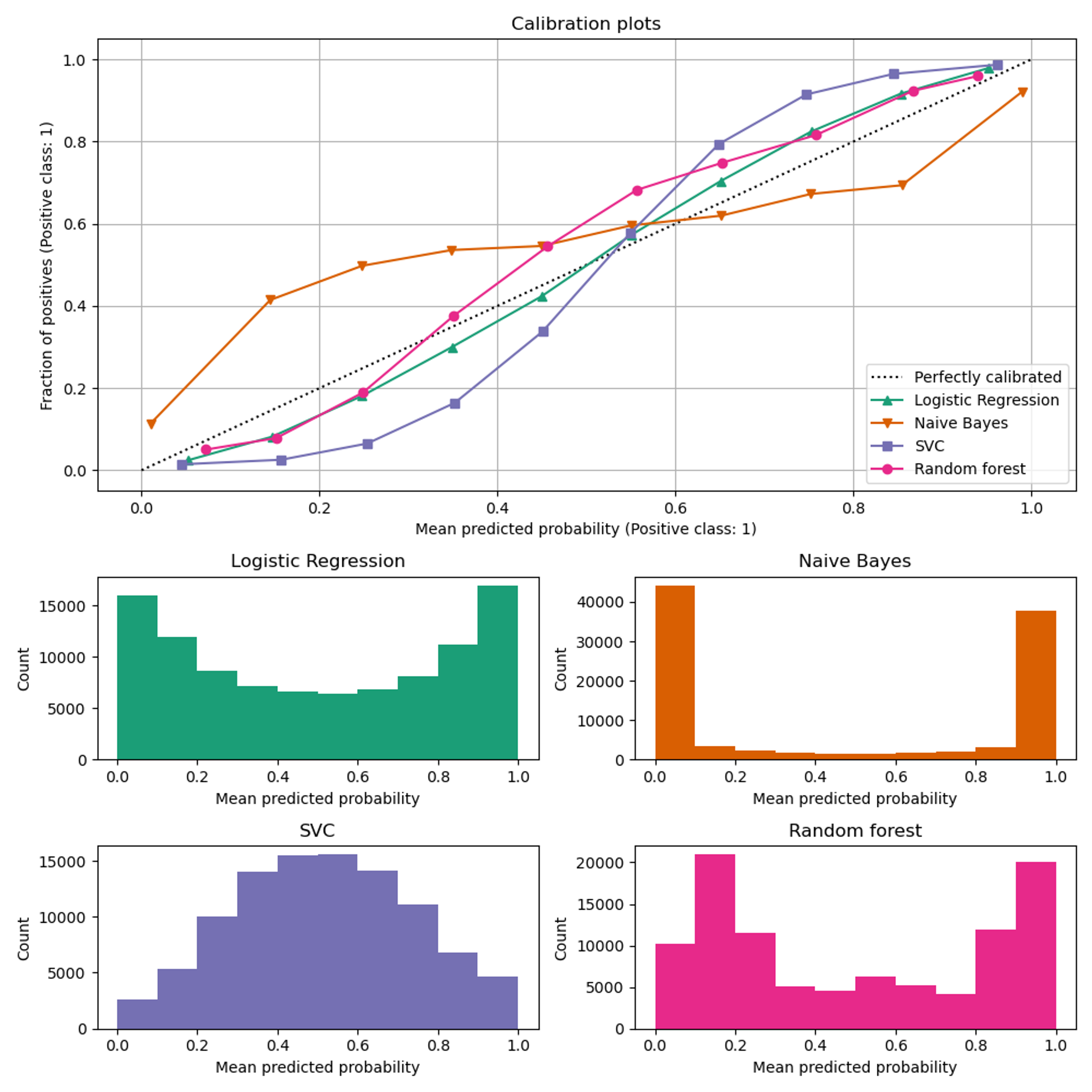
将预测值升序排序, 然后划分bin, “ x-axis represents the average predicted probability in each bin” . 而y轴则是对应bin中, 相应样本是正样本的比例, 然后绘制相应曲线

对于条形图的解释

• 逻辑回归的结果很不错, 几乎是可以开箱即用, 是因为本身其loss就是交叉熵, 使用的概率.或者从另一个角度就是最大似然估计.

• 贝叶斯看起来更加倾向于将输出close to 0 or 1, 主要可能是因为（存疑）其假设特征是独立的.

• 随机森林有一个明显的特点就是, 输出close 0.1 or 0.9 , Niculescu-Mizil and Caruana [3] 认为, 由于随机森林是bagging模型, 如果想让一个样本严格输出为0, 那么就意味着, 所有的base 决策树都要预测这个样本为0, 这通常是不可能的, 因为单个树具有高方差（可能会引入噪声）, 以及最后预测输出的时候是多个树average, 所以结果通常来说不会是 0 or 1

  • 什么是高方差？

    通常来说, 高方差指的是, 模型相对复杂, 从而完美的匹配了训练集的数据, 只学到了局部的模型（距离“平均模型”比较远, 方差大）, 即过拟合, 这使得模型对数据很敏感（因为数据可能也是局部的）.

    为什么单个树的方差很高？

    单个决策树具有高方差的原因主要与其自身的结构和学习方式有关.以下是一些导致决策树高方差的关键因素(Chatgpt语气)：

    1. 不剪枝：决策树在构建过程中会持续分裂节点, 直到满足某个停止条件.如果决策树没有适当的剪枝策略, 它会继续生长并尝试完美地拟合训练数据, 包括数据中的噪声和异常值.这种过拟合行为会导致模型对训练数据的微小变化非常敏感, 从而增加了方差.
    2. 贪婪搜索：决策树的构建通常基于贪婪搜索策略, 这意味着在每个节点上, 它会选择局部最优的特征进行分裂, 而不是考虑全局最优解.这种局部最优选择可能导致树过于复杂, 进而增加了模型的方差.
    3. 数据噪声和异常值：由于决策树是基于数据特征进行分裂的, 数据中的噪声和异常值可能会对树的结构产生不成比例的影响.这些数据点可能会导致树在错误的方向上进行分裂, 从而增加了模型的方差.
    4. 特征选择的随机性：在构建决策树时, 通常会从特征集中选择一个特征进行节点分裂.如果没有适当的随机性引入, 即使是很小的数据变化也可能导致选择不同的特征, 从而产生完全不同的树结构, 增加了模型的方差.
    5. 树的深度：决策树的深度也会影响其方差.树越深, 模型就越有可能学习到数据中的噪声和偶然规律, 从而导致高方差.
    6. 数据表示的选择：决策树对数据的表示非常敏感.如果数据的特征没有经过适当的预处理和特征工程, 可能会导致树对数据的某些特定表示过度拟合, 从而增加方差.

    当这些高方差的树被集成在一起时，由于它们的随机性质，它们彼此之间存在差异。这种差异导致它们在某些数据点上出现错误，但在其他数据点上正确，因此这些错误会相互抵消。通过集成多个具有高方差的模型，随机森林能够平均化这些错误，从而降低整体的方差。

• SVM则是属于那种“差不多就行”、“能分类正确即可”, 因此模型输出大多数在0.5 左右

2. Calibrating a classifier

2.1 函数介绍

使用 CalibratedClassifierCV 来实现校准 , 这个类使用交叉验证来校准模型.首先要注意的是, 校准模型时使用的训练集, 不能和 用来训练未校准模型的训练集一样.同时也是为了样本分布平衡, 需要让校准模型的过程在不同训练子集上重复.其核心思想为：

• When ensemble=True (default)
  • data is split into k (train_set, test_set)
  • 然后 CCV类中的base_estimator（比如决策树）, 首先独立的复制k份, 分别在相应的 train_set 上进行训练, 然后在相应的test_set 的预测结果, 会进一步被用来 fit a calibrator (either a sigmoid or isotonic regressor). each calibrator maps the output of its corresponding classifier into [0, 1].
  • fit 好后的 calibrator 存在calibrated_classifiers_ attribute, where each entry is a calibrated classifier with a predict_proba method that outputs calibrated probabilities.
  • 然后 CCV 这个类本身有一个函数：predict_proba , 调用时结果为：average of the predicted probabilities of the k estimators in the calibrated_classifiers_ list.
  • The output of predict is the class that has the highest probability.
• when ensemble=False
  • 一眼丁真, 鉴定为最好别用

2.2 校准方法

2.2.1 sigmoid 方法

\[p(y_i = 1 | f_i) = \frac{1}{1 + \exp(A f_i + B)}\]

A and B are real numbers to be determined when fitting the regressor via maximum likelihood.

该方法适用于

• calibration error is symmetrica
  • meaning the classifier output for each binary class is normally distributed with the same variance
  • This can be a problem for highly imbalanced classification problems, where outputs do not have equal variance.
• small sample sizes
• un-calibrated model is under-confident and has similar calibration errors for both high and low outputs.

2.2.2 isotonic 方法

fits a non-parametric isotonic regressor, which outputs a step-wise non-decreasing function, see sklearn.isotonic. It minimizes:

该方法输出map function 是 严格单调递增的 : 即未校准的模型 认为 p(A) < p(B) , 那么经过校准后的的 p(A) 应该还是小于 p(B)

\[\sum_{i=1}^{n} (y_i - \hat{f}_i)^2\]

subject to

\[\hat{f}_i \geq \hat{f}_j\]

whenever

\[f_i \geq f_j\]

$y_i$ is the true label of sample and $\hat{f}_i$ is the output of the calibrated classifier for sample (i.e., the calibrated probability).

Overall, ‘isotonic’ will perform as well as or better than ‘sigmoid’ when there is enough data (greater than ~ 1000 samples) to avoid overfitting

 It is not advised to use isotonic calibration with too few calibration samples (<<1000) since it tends to overfit.

References

[1] Sklearn-calibration

[2] 模型校准(Calibration of Models)技术