Perplexity

0. 前言

在 NLP 中, 经常可以看到使用”困惑度”来描述一个 LLM 的能力. 那么什么是”困惑度”?

简单理解, 困惑度就是”模型对样本预测结果的信心”. 具体的, 模型对这个样本结果的预测概率越高, 表明信心越高, 对应困惑度越低.

本文介绍的Perplexity 特指 “Perplexity of a probability model”.

1. 举个栗子

假设我们的 vocabulary 就只有6个单词, “a”, “the”, “red”, “fox”, “dog”, and “.” . 模型需要从这里边预测输出句子 W : "a red fox ."

\[\begin{align*} P(W) & = P(w_1, w_2, \ldots, w_n) \\ & = P(w_n|w_1, w_2, \ldots, w_{n-1}) \times P(w_1, w_2, \ldots, w_{n-1}) \end{align*}\]

对于这句话就是:

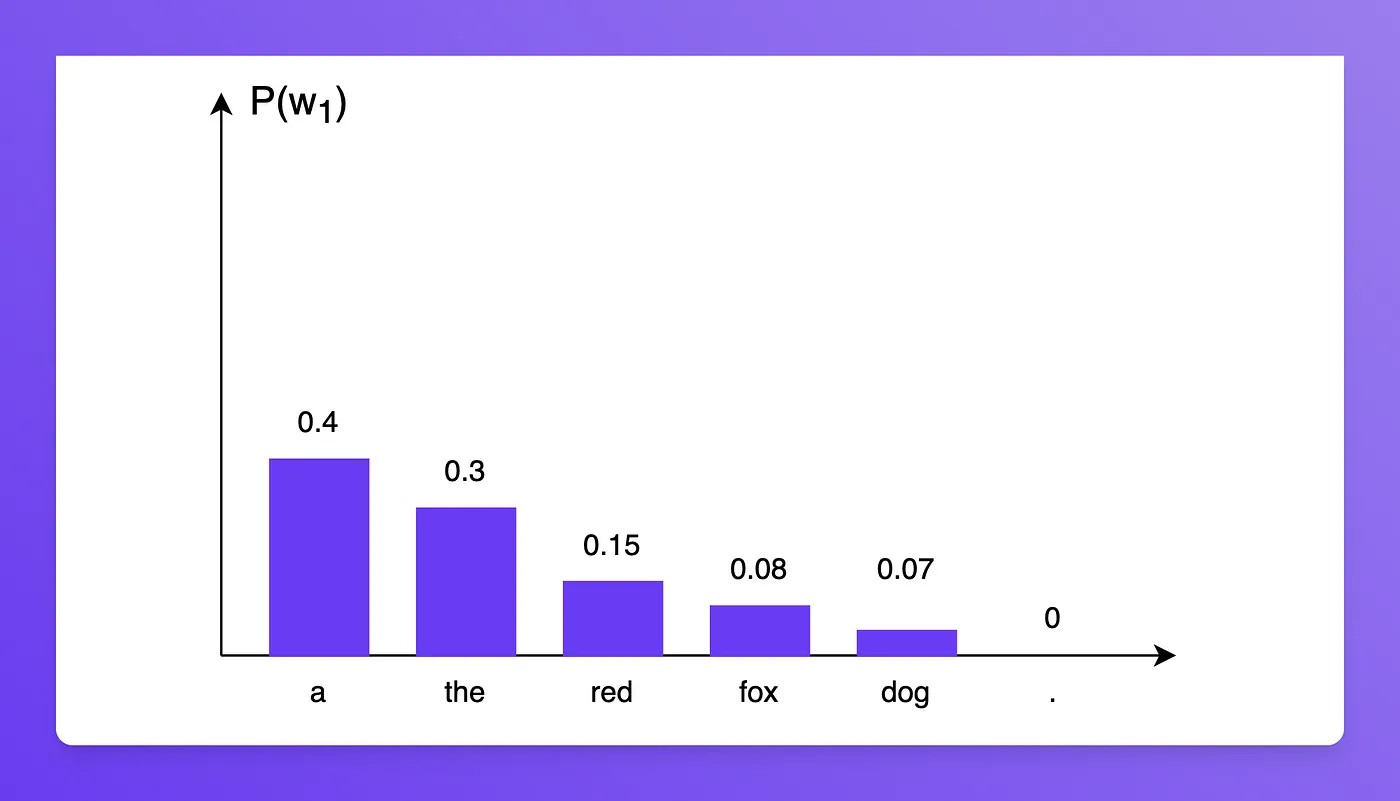
\[\begin{align*} P(' a\ red\ fox\ . ') = P(' a ') \times P(' red ' | ' a ') \times P(' fox ' | ' a\ red ') \times P(' . '|' a\ red\ fox ') \end{align*}\]

假设模型, 预测第一个字的概率分布如下 :

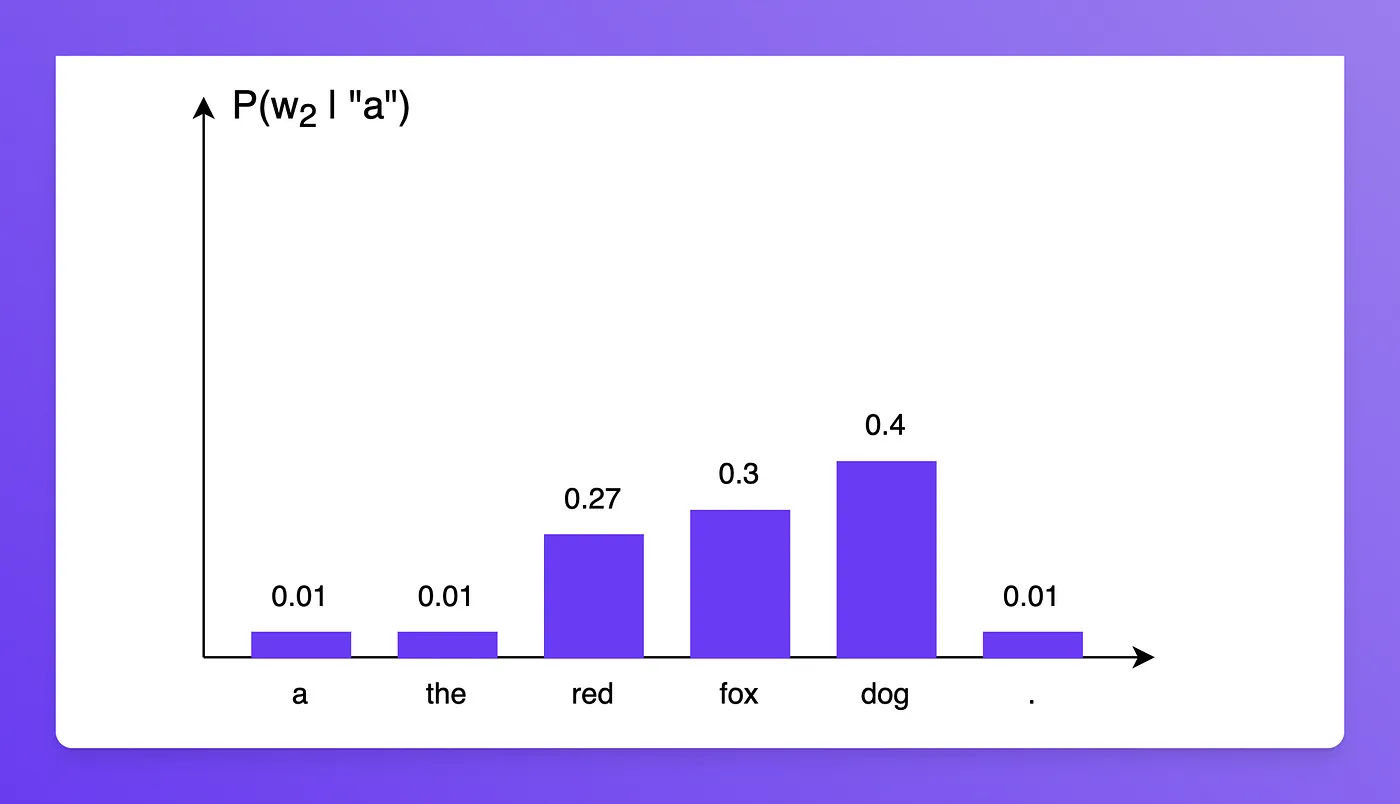
则有 $P( ‘ a ‘ ) = 0.4$ , 进一步的 $P( w_2 | ‘ a ‘ )$ 分布如下

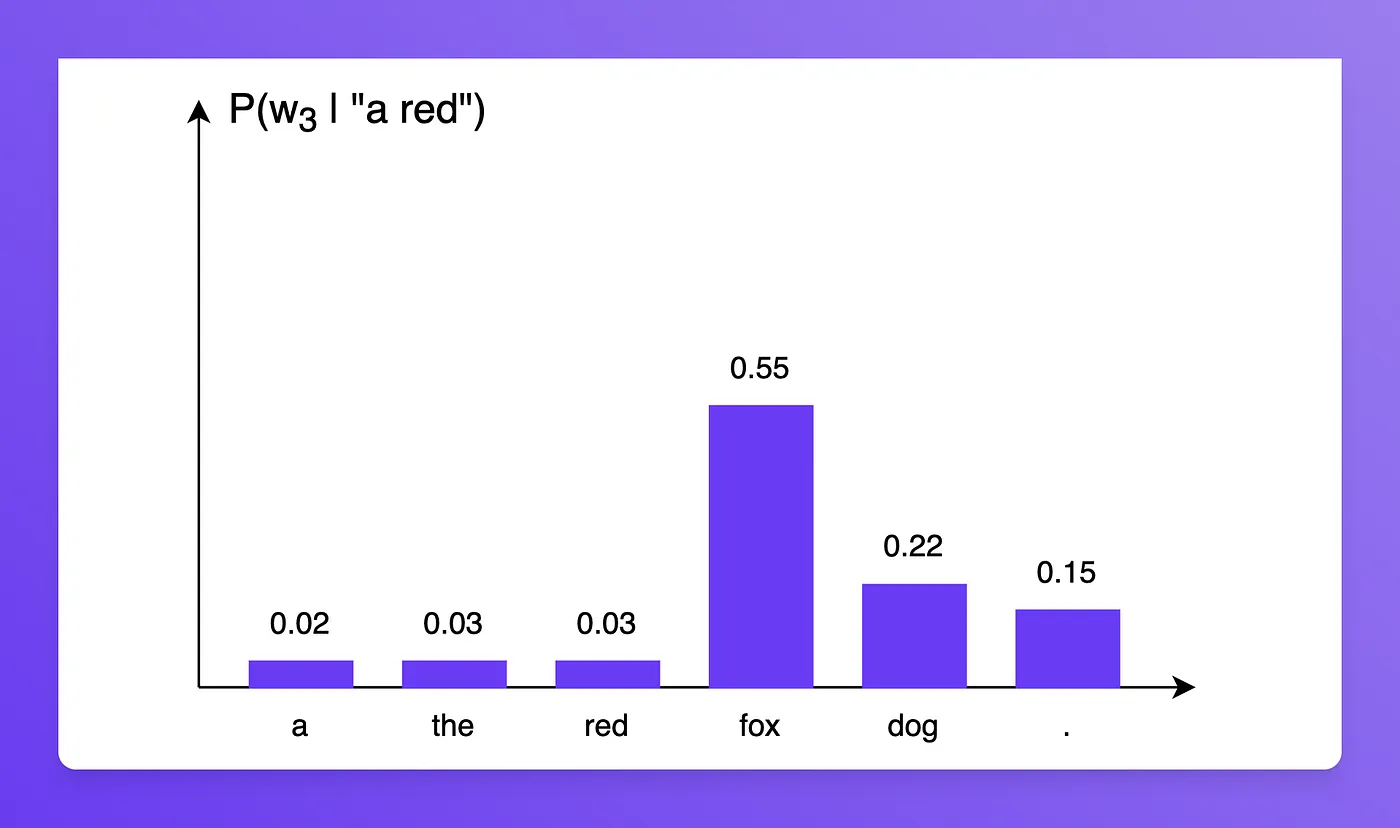
于是 $P( ‘ red ‘ | ‘ a ‘ ) = 0.27$ , 同理, 根据以下分布

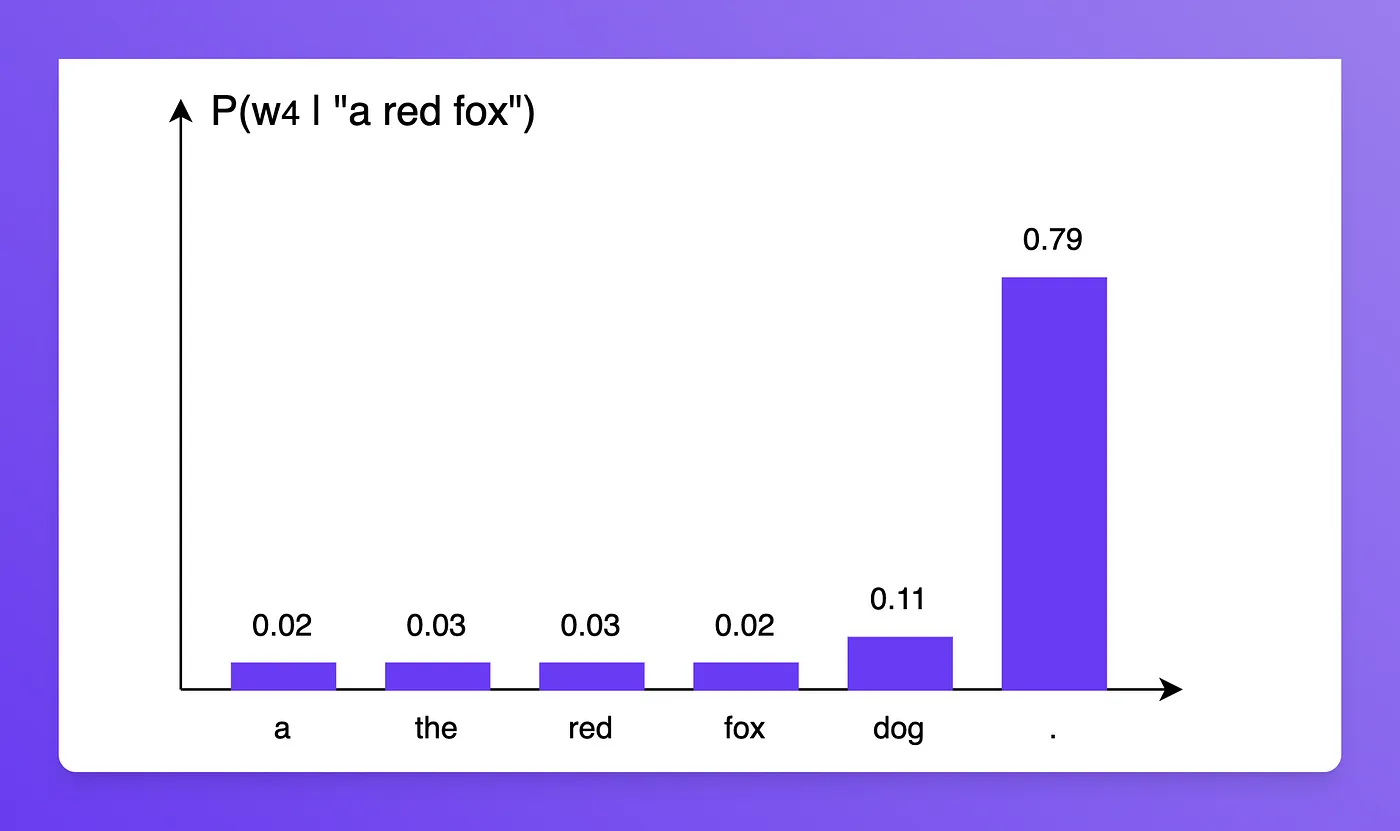
我们有如下结果:

\[\begin{align*} P(' a\ red\ fox\ . ') &= P(' a ') \times P(' red ' | ' a ') \times P(' fox ' | ' a\ red ') \times P(' . '|' a\ red\ fox ') \\ &= 0.4 * 0.27 * 0.55 * 0.79 \\ &= 0.0469 \end{align*}\]

0.0469则表示当前这个模型对于预测 “a red fox.” 的信心如何, 不过有一个问题 : 因为这个信心是概率的连乘, 于是导致理论上, 句子越长, 信心越小. 因此需要进行一个 “Normalize”的操作 . 我们可以使用 几何平均数 来实现上述功能, 从而得到一个新的量化标准:

\[P_{norm}(W) = P(W)^{1/n}\]

这里的n表示句子的单词(token)数量.于是

\[\begin{align*} P_{norm}('a\ red\ fox\ .') &= P('a\ red\ fox\ .')^{1/n} \\ &= 0.0469 ^ {1/4} \\ &= 0.465 \end{align*}\]

这样我们就可以使用 $P_{norm}$ 来度量模型对不同长度句子的预测输出”信心”.

2. 如何计算

前边我们提到, 模型与输出的句子, 信心越足, 困惑度越小. 可以看到, 困惑度的计算公式如下:

\[\begin{align*} PP(W) &= \frac {1} {P_{norm}(W)} \\ &= \frac {1} {P(W)^{1/n}} \\ &= (\frac {1} {P(W)}) ^{1/n} \\ &= P(W) ^{-1/n} \end{align*}\]

对于之前的这个模型, 其 $PP(W) = (1/0.0469)^{1/n} ≈ 2.15 $

而假设有另外一个模型, 给定任意条件下, 对下一个单词的预测概率均相等为 1/6 . 那么这个模型的的困惑度为:

\[PP(W) = (\frac {1} {(1/6)^4}) ^{1/4} = 6\]

明显比之前的模型困惑度更高, 表明这个模型 更差 , 因为这个模型就是随机输出.

3. 和交叉熵的关系

我们知道, 香农熵 计算方式为 :

\[H(p) = - \sum_{i=1}^{n} p\ log_2\ p\]

交叉熵的计算方式:

\[H(p, q) = - \sum_{i=1}^{n} p\ log_2\ q\]

事实上: \(KL(p, q)\ =\ -H(p)\ +\ H(p, q)\)

对$PP(W)$进行拆解, 得以下式子:

(1) 注意之前是 n , 强调一个句子. 这里是 N , 强调模型对整个vocabulary的输出分布

(2) 最后的 q分布 就是下一个单词的分布, 是一个 One-hot 向量

\[\begin{align*} P(W) ^{-1/ N} &= \prod_{i=1}^{N} P(w)^{- 1/N} \\ &= P(w_1)^{- 1/N} * P(w_2)^{- 1/N} * ... * P(w_N)^{- 1/N} \\ &= 2 ^ { - \frac 1 N\ \sum_{i=1}^{N} \ log_2\ p } (忽略常数 2^{-1/N}) \\ &= 2 ^ {\ H(P , \ q)} \end{align*}\]

从这个角度来看, 困惑度越小, 交叉熵越小, 预测越准确.

最后, 实际计算过程中, 可能使用以e为底的对数, 也有计算其log后作为困惑度, 此外还有一些其他计算方式, 但是本质类似, 就是想表达 “预测输出的概率越大, 困惑度就越小”

Reference

[1] Two minutes NLP — Perplexity explained with simple probabilities

[2] Wiki-Perplexity

[3] Perplexity Intuition (and its derivation)