L1 and L2 Regularization
0. 前言
在机器学习或深度学习中,无论是分类、回归还是其他场景,通常都是利用模型去拟合一个函数。在这个过程中,正则化是一种常用的手段,用来防止过拟合。本篇博客主要从几个角度探讨正则化的理解,并解释它为何能够防止过拟合。
阅读前, 需要你 : 有高数基础知识, 线代基础知识, 统计学习基础知识, 当然还要有 ML和 DL 的知识背景.
1. 公式
给定输入 $x_1,x_2…x_n$ 和输出 $y_1,y_2…y_n$, 我们通过一个模型(函数) $f(w,x)$ 来 $map$ 输入输出之间的关系.其中 $w$ 表示模型的参数 . 函数参数的寻求通过优化以下 $loss function$
\[L = \sum_{i} L(x_i,y_i) + R(w)\]这里 $R(w)$ 是关于参数 $w$ 的一个函数.对于 L1 Regularization
\[R(w) = \lambda {\|w\|_1}^2\]对于 L2 Regularization
\[R(w) = \lambda {\|w\|_2}^2\]2. 理解
从式子上看, Regularization 看起来就是想让参数 $w$ 的范数小一点 , 下面来看为什么 $w$ 的范数小一点, 就能减缓过拟合.
首先我们来看过拟合是什么? 定义这里就不说了, 直观看个图吧.
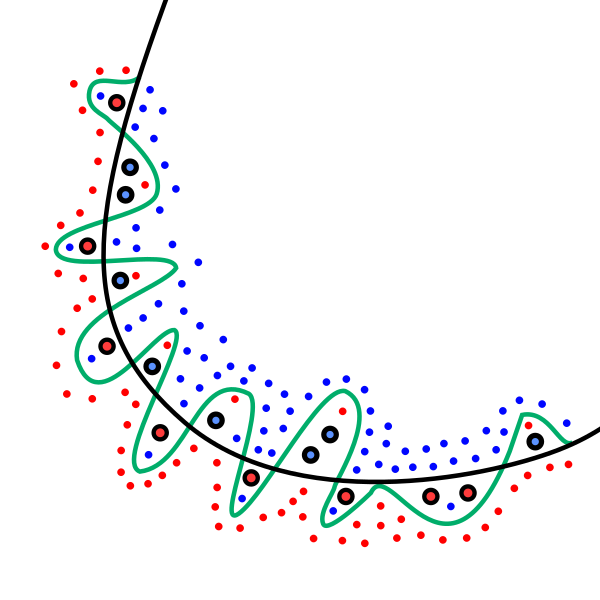
上图中,我们有蓝色和红色,2组类别的数据点, 想训练一个分类器f(w,x)去将蓝色点和红色点分开.
可以看到, 绿色的线($f_1$)近乎完美的对数据进行了拟合, 黑色($f_2$)的看起来差一些.
但是啊, 我是说有没有一种可能, 这个数据集他有异常点(比如加粗的那几个), 如果你拟合的太好, 反而会把噪声也拟合了, 导致你的模型泛化性能不好. 反观黑色的线, 就看起来更加不错.
那么如何才能让模型从绿色变成黑色的线呢? 即怎么把函数的”弯弯绕绕”给他拿走.
我们对函数 $f(x)$ 在某个点进行泰勒展开:
\[f(w,x) = f(w,a) + f'(w,a)(x - a) + \frac{f''(w,a)}{2!}(x - a)^2 + \cdots\]可以看到, 一个函数的复杂度(就是”弯弯绕绕”), 其实来自于它的高阶项 $ f^n(w,a)(x - a)^n$ . 比如 二次函数就1个弯, 三次函数就2个弯了, 同理次幂越高,”弯弯绕绕”越多. 因此想把高阶项拿掉, 其实可以让其系数 : $f^n(w,a) -> 0$ , 而系数正好就是 $w$ 的函数.
我们有理由相信,如果 $w$ 不是很大的情况下, $f(w)^n$ 应该不会大到哪里去.于是就把 $w$ 的范数加到loss中, 去让 $w$ 小一点.
3. 等价形式
3.1 给权重 $w$ 加约束
让 $w$ 小一点等价于让 $w$ 不太大 - 鲁迅
所以优化目标可以变为:
\[minimize \ L(w,x) , \ s.t. {\|w\|_2}^2 \leq C\]使用拉格朗日乘数法, 上述问题变为:
\[\mathop{minimize}\limits_{w} \ \mathop{maximize}\limits_{\lambda} \ L(w,\lambda,x) = L(w) + \lambda ( {\|w\|_2}^2 - C)\]剩下过程就是,求导等于0, 然后计算相应的 $w$ 和 $\lambda$ 即可. 不过这里想说的是, 在对 $w$ 求导的时候, 你会发现其实并没有 $C$ 的事情 :
\[\frac{\partial J}{\partial w} = \frac{\partial L}{\partial w} + 2 * \lambda w\]于是不妨直接 $minimize$ 下式:
\[minimize \ L(w,x) + \lambda {\|w\|_2}^2\]1范数同理, 不再赘述.
3.2 让权重 $w$ 衰减
\[minimize \ J = \ L(w,x) + \lambda {\|w\|_2}^2\]梯度下降:
\[\begin{align*} w &= w - \eta ( \frac{\partial L}{\partial w} - 2 * \lambda w) \\ &= (1 - 2 * \lambda * \eta ) w - \frac{\partial L}{\partial w} \\ \end{align*}\]当 $2 * \lambda * \eta \in (0,1)$ 的时候, 每次更新权重都是在上一次权重衰减后的基础上进行的.
3.3 给权重 $w$ 限定分布
从统计学上来看, $f(w,x)$ 输出的是一个分布去拟合 y 的分布 , 使用贝叶斯公式:
\[p(w|x,y) = \frac{p(w) * p(x,y|w)}{p(x,y)}\]$p(x,y)$ 是死的, $maximize \ p(w|x,y)$ 就是 $maximize$ 分子
极大似然估计 : $\mathop{arg \ max}\limits_{w}\ p(w|x,y) = \mathop{arg \ max}\limits_{w} \ p(x,y|w)$.
极大似然估计不关心 w 的原始分布. 它的核心思想是,假设数据是由参数 w 生成的,那么反过来,能让根据这些数据计算出的 w 的条件分布, 最大的那个 w 就是我们要找的 w.
最大后验估计: $\mathop{arg \ max}\limits_{w} \ p(w|x,y) = \mathop{arg \ max}\limits_{w} \ p(x,y|w) * p(w)$.
最大后验估计对极大似然估计说: 老弟你这不对, 分子最大化的时候 , 你得考虑 p(w) .
OK , 基于最大后验估计, 取 log 得到:
\[\begin{align*} \mathop{arg \ max}\limits_{w} \ p(x,y|w) * p(w) &= log \ p(x,y|w) + log \ p(w) \end{align*}\]我们不看前半部分,只看后半部分.
- 假设 $w \sim N(0 , \sigma ^ 2)$
则
\[\begin{align*} maximize \ log \ p(w) &= \\ &= maximize - \frac {1} {2 \sigma ^2} {\|w\|_2}^2 + C \\ &= minimize \ \frac {1} {2 \sigma ^2} {\|w\|_2}^2 + C \\ &\equiv minimize \ {\|w\|_2}^2 \ (\sigma = 1) \end{align*}\]从这个角度可以看到, 如果加 L2 Regularization , 其实就是对 model 的权重参数 $w$ 假定了先验分布为标准正态分布.
- 假设 $w \sim Laplace(0 , b)$
则
\[\begin{align*} maximize \ log \ p(w) &= \\ &= maximize - \frac {1} {2 b} {\|w\|_1}^2 + C \\ &= minimize \frac {1} {2 b} {\|w\|_1}^2 + C \\ &<=> minimize \ {\|w\|_1}^2 \ (b = 1) \end{align*}\]从这个角度可以看到, 如果加 L1 Regularization, 其实就是对 model的权重参数 $w$ 假定了先验分布为拉普拉斯分布.
4. 区别
4.1 函数性质
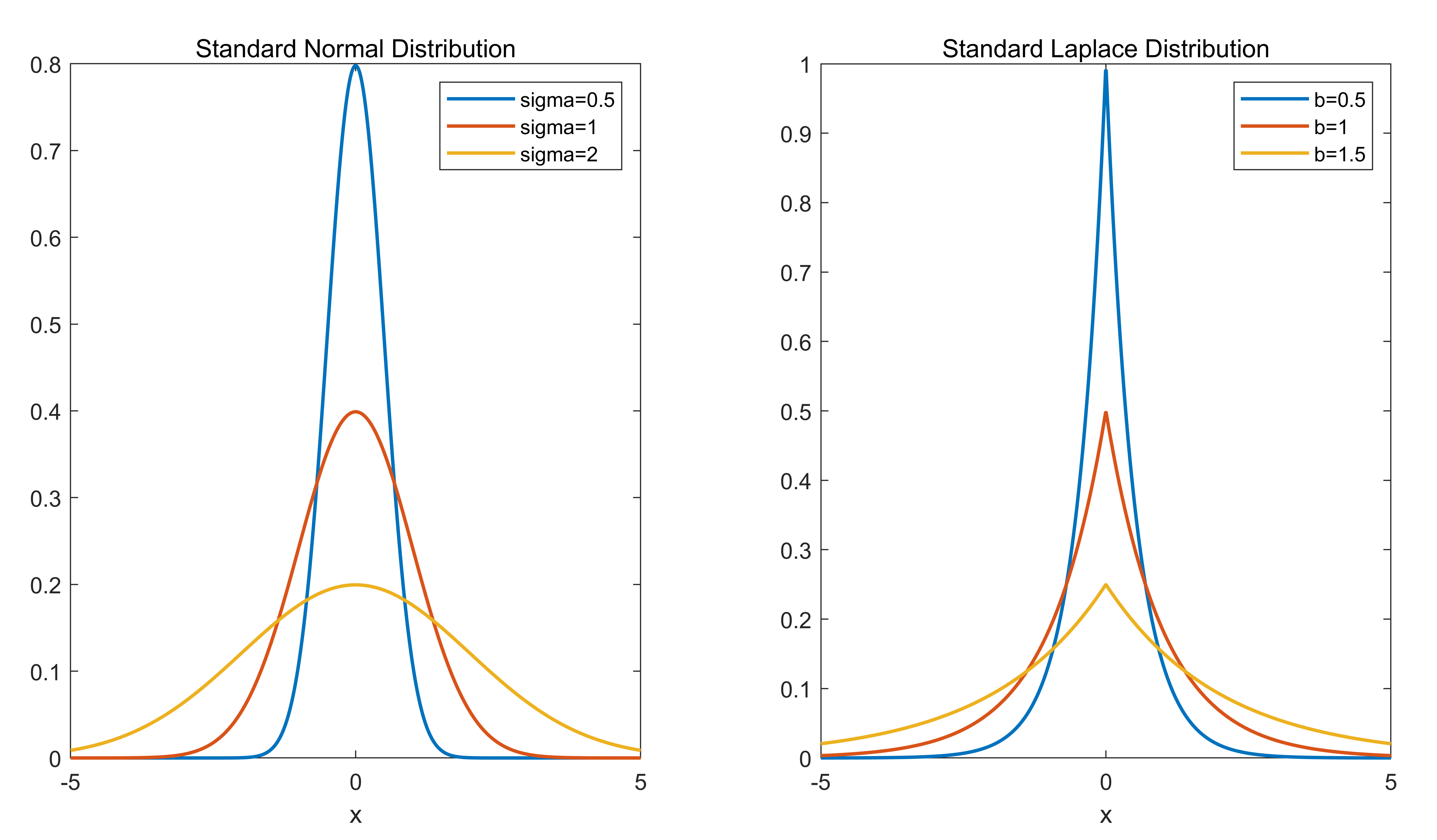
我们可以从标准正态分布和拉普拉斯分布的函数性质,来窥探L1 Regularization 和 L2 Regularization 的区别.
根据上图可以看到, L1 Regularization (拉普拉斯分布) 在 0 附近形状更尖锐, 将 w 推向0的时候更加强硬. 而 L2 Regularization (标准正态分布) 显得更加柔和.
4.2 几何性质
此外也可以从几何性质上对 L1 Regularization 和 L2 Regularization 进行分析.
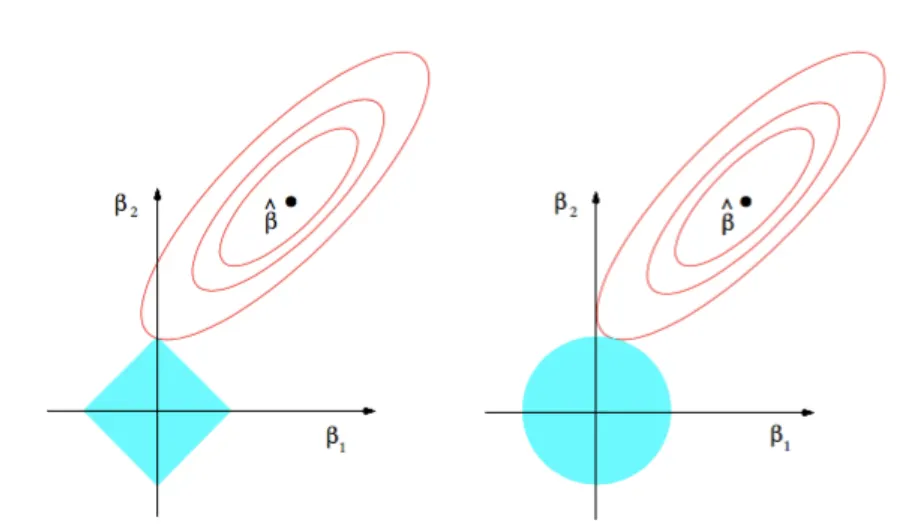
1范数在几何上表现为一个高维的四方体,2范数则是一个高维的球体. 可以从上图看到,在做minimize时候,L1 Regularization 的 “尖儿” 更容易触到靠内的等高线,即 “尖儿”的位置具有更低的值, 而 “尖儿”的位置,就意味着 w 的某个分量就是0. 而2范数因为整个表面都是外凸出的弧,在哪个地方都有可能取得最小值.
这也就是为什么说, L1 Regularization 能够比 L2 Regularization 更加的 “Sparsity”.所以 L1 正则项的另外一个应用就是能够进行特征选择: LASSO回归通过在原始损失函数上添加 L1 Regularization,导致特征 $i$ 对应的权重 $w_i$ 为 0, 我们认为, 权重 $w_i=0$ 的特征就是可以去除的.