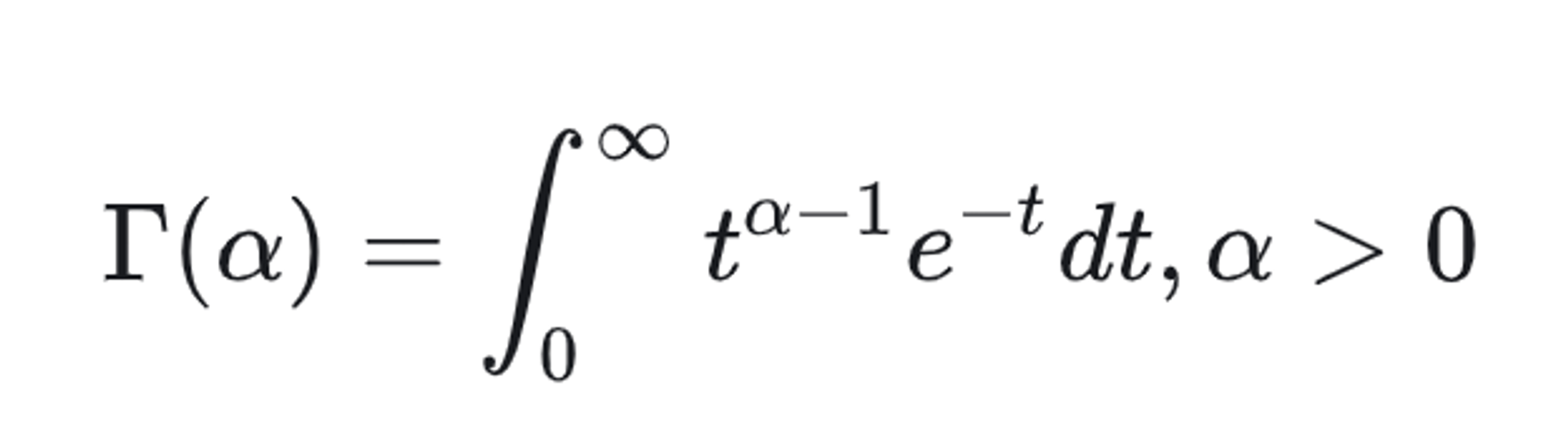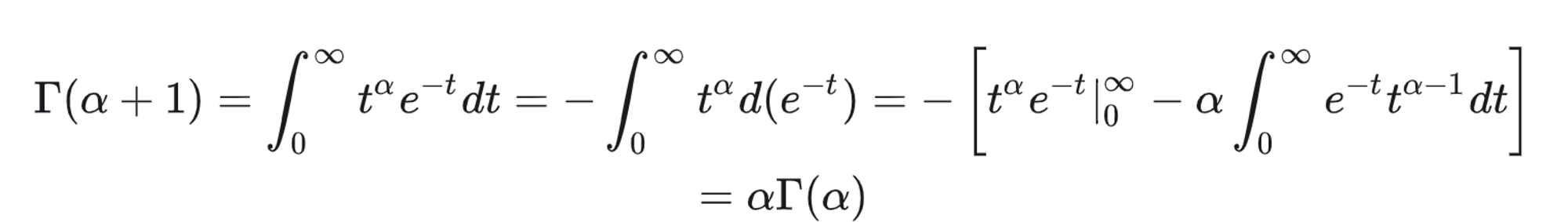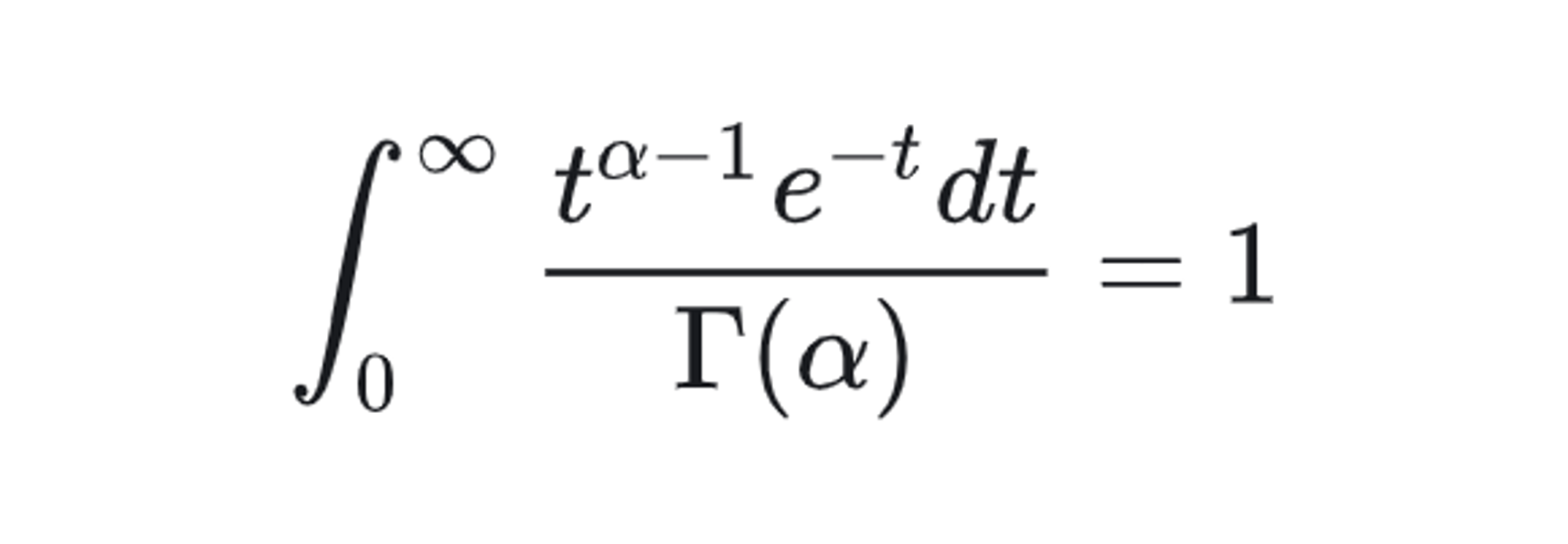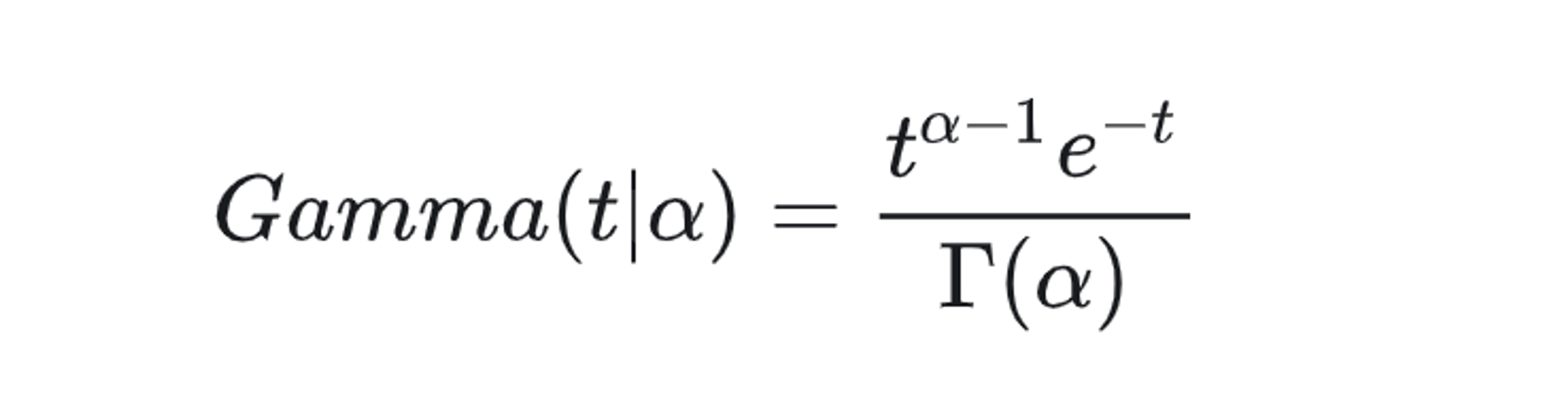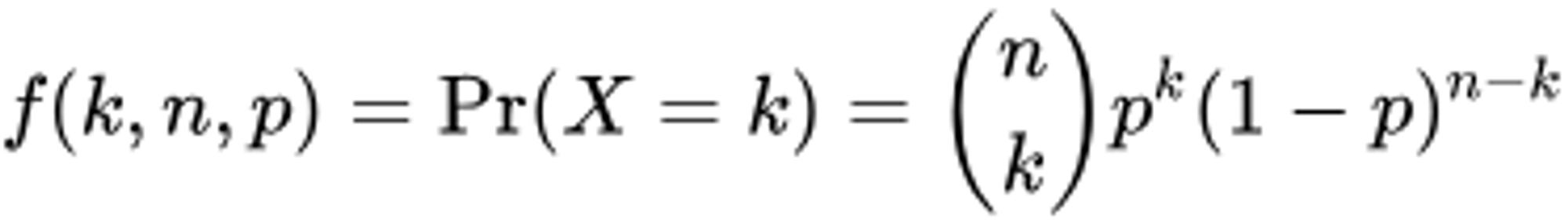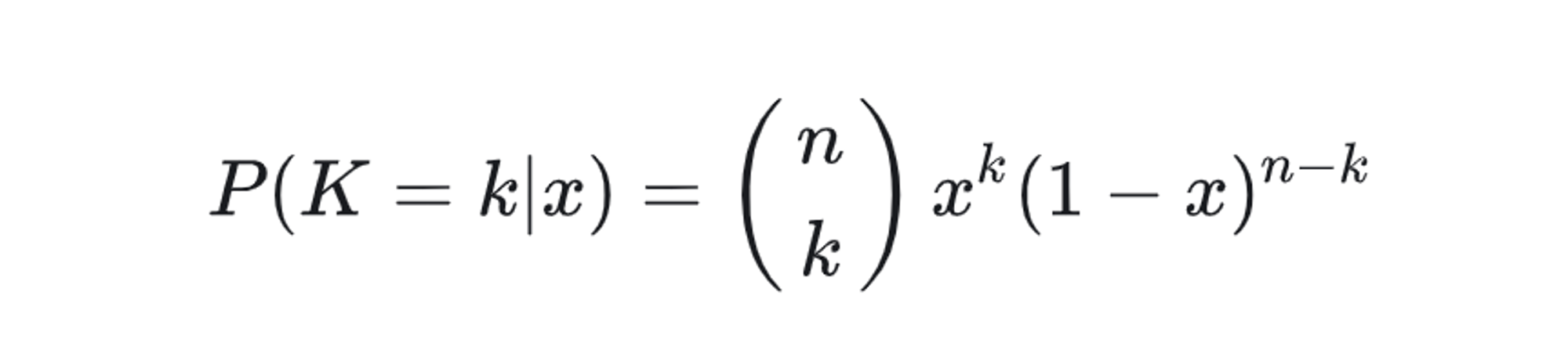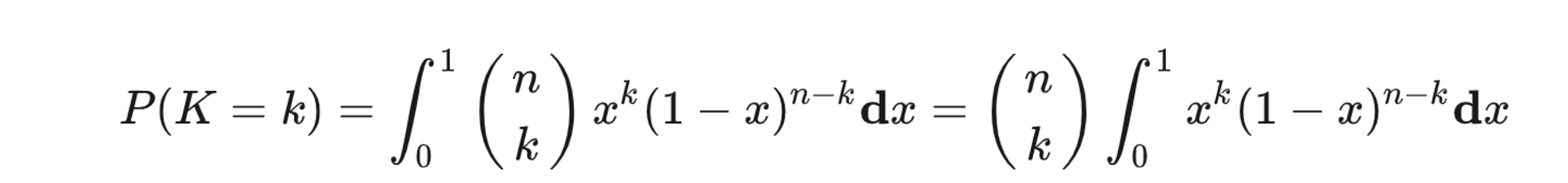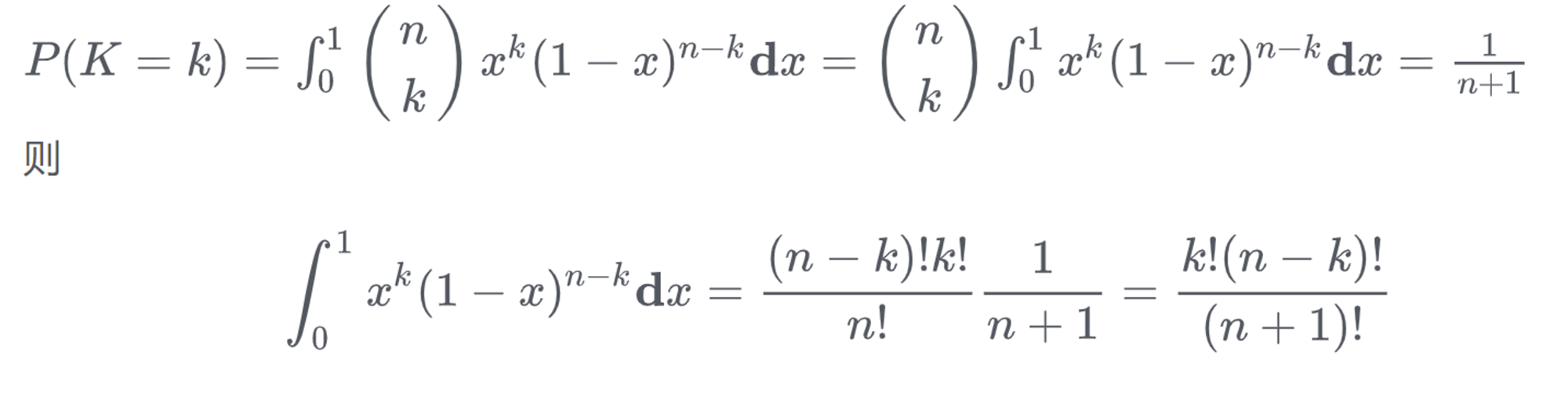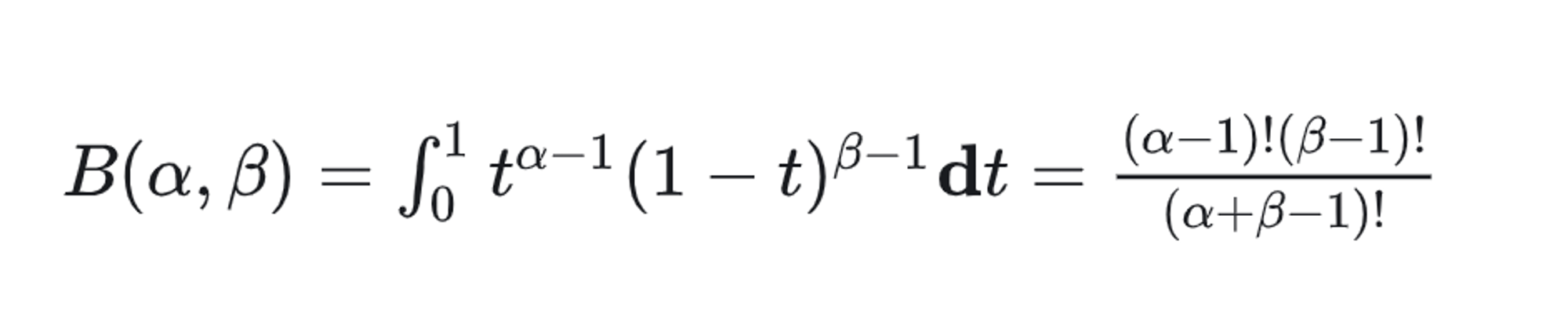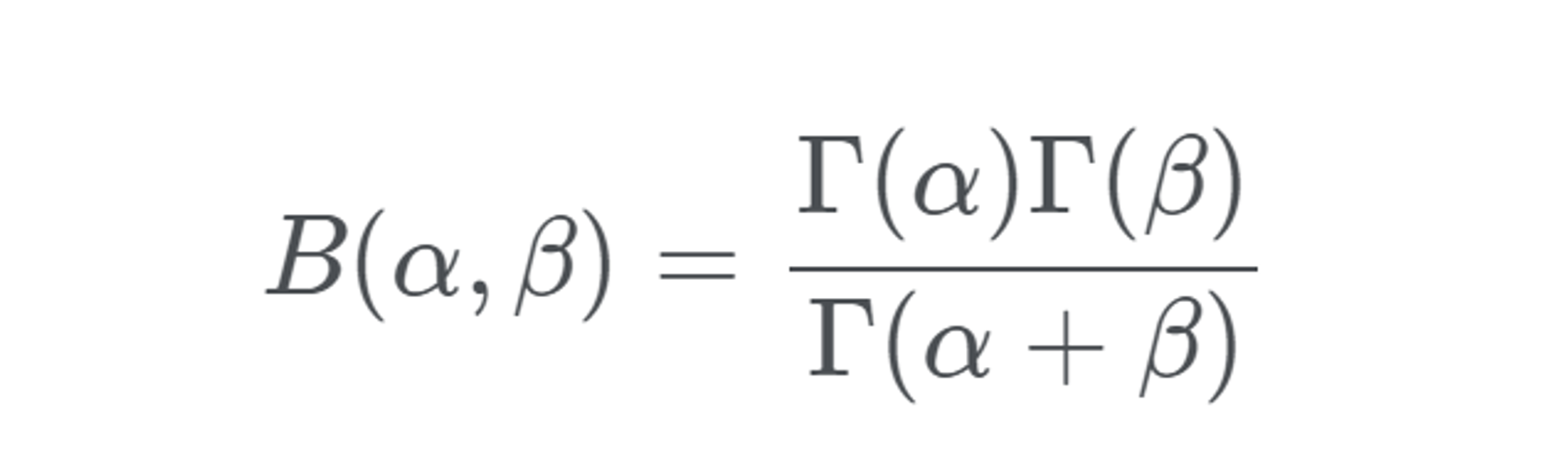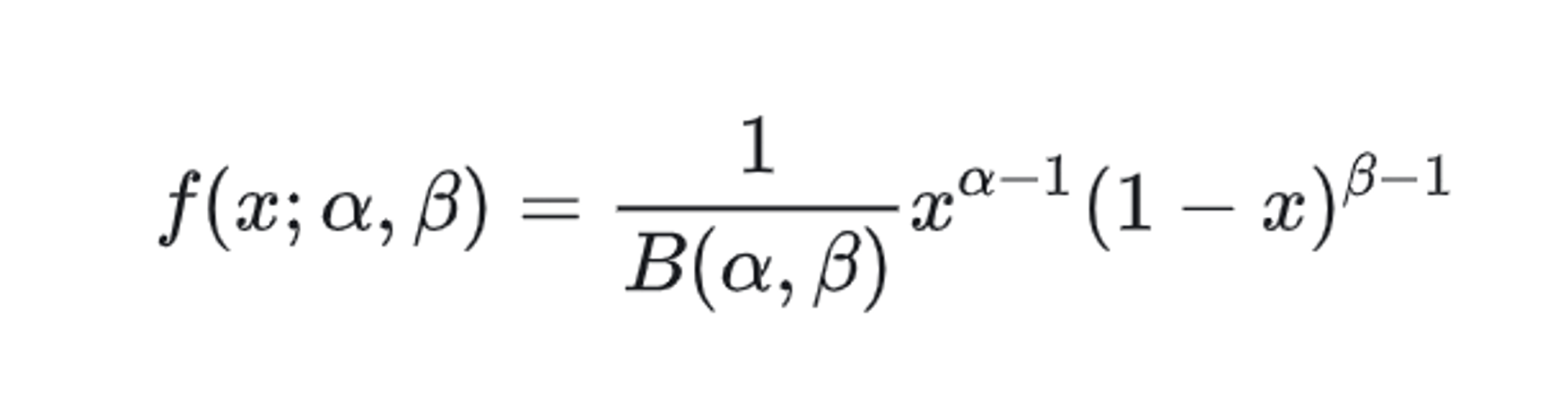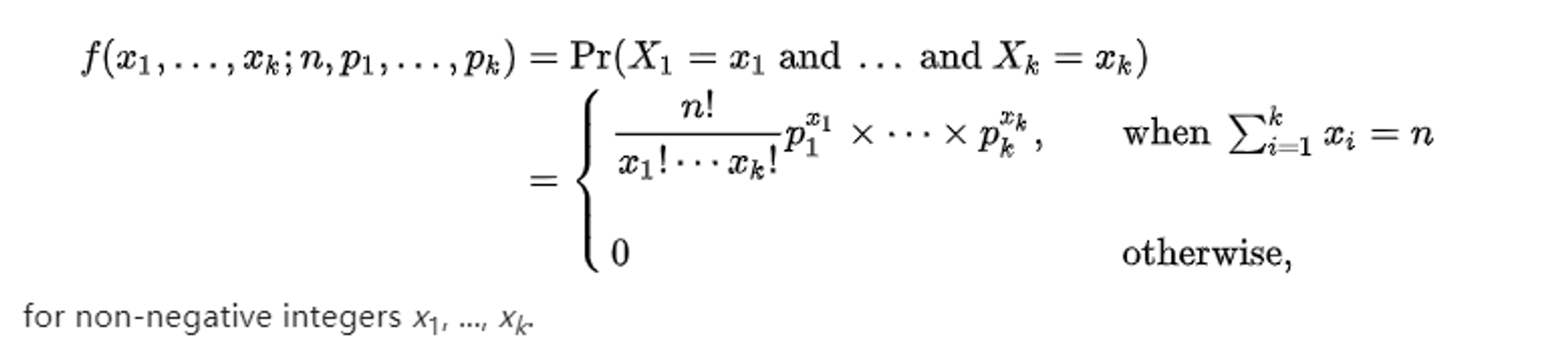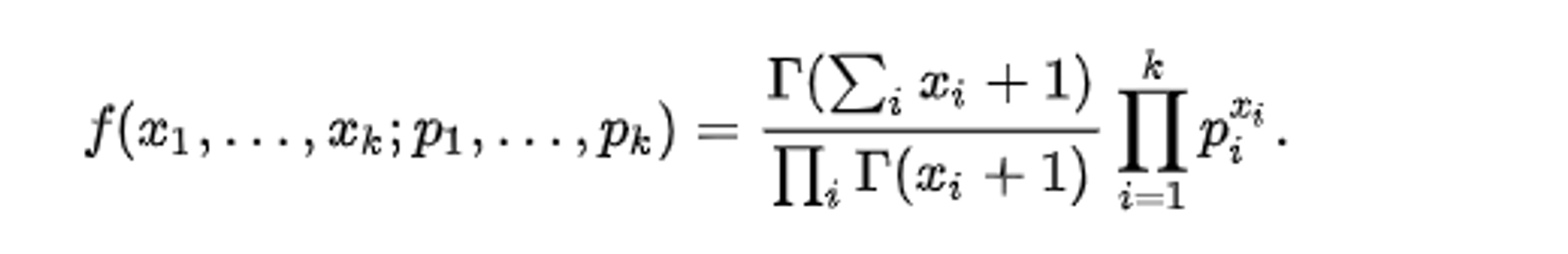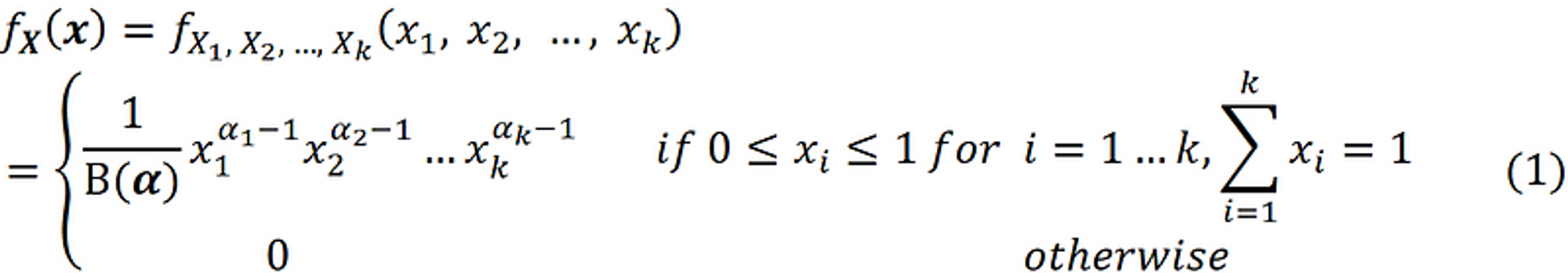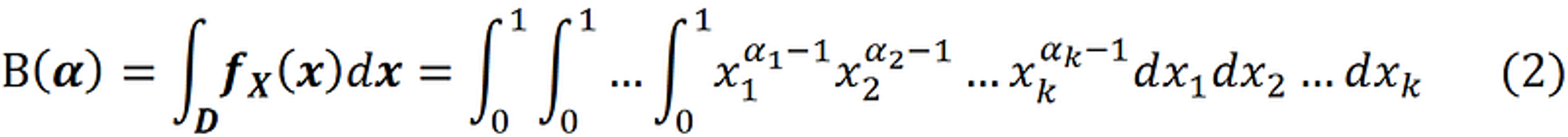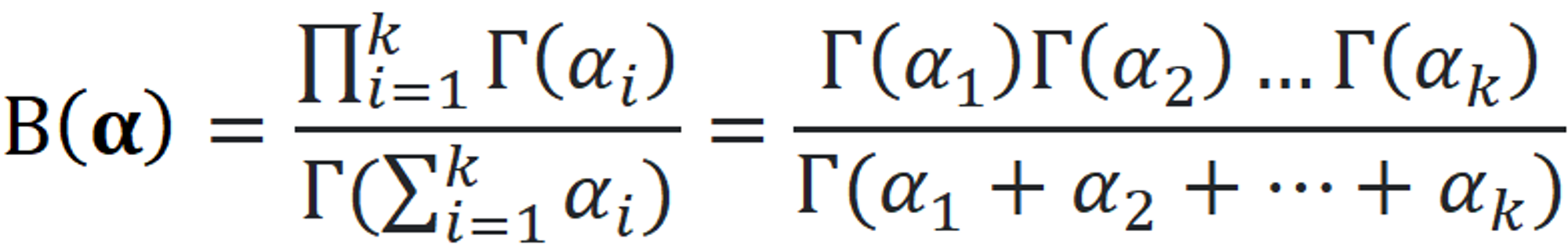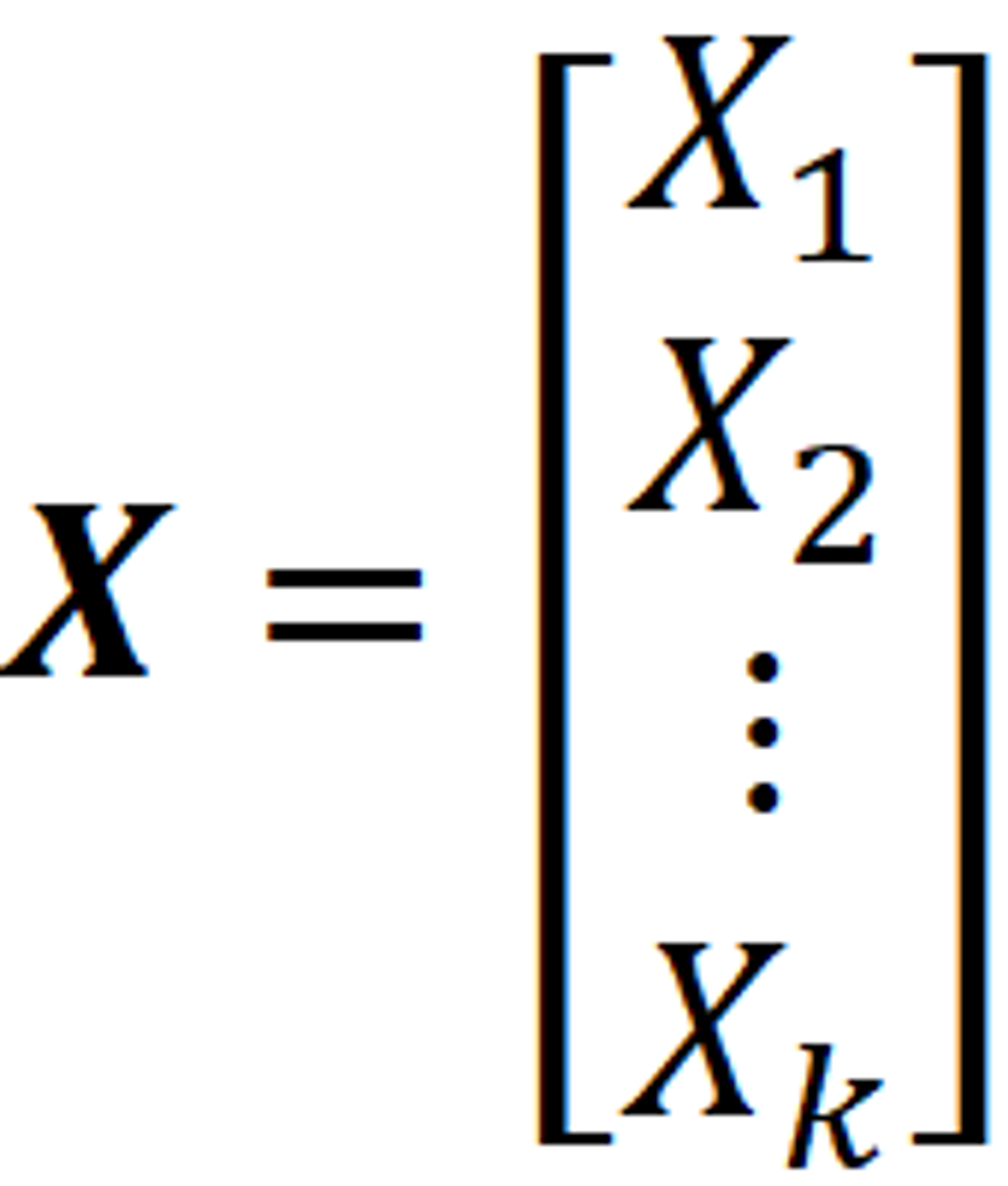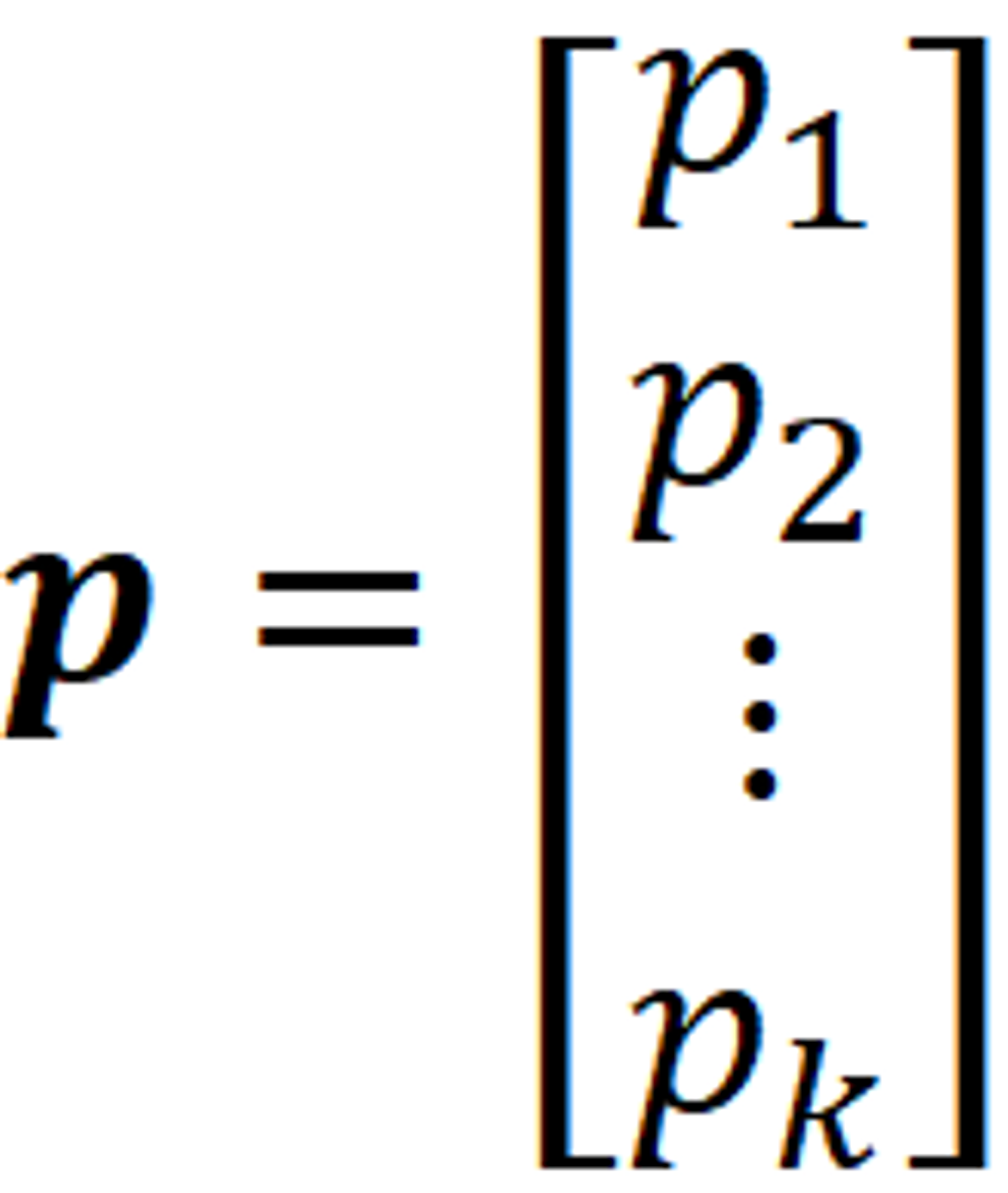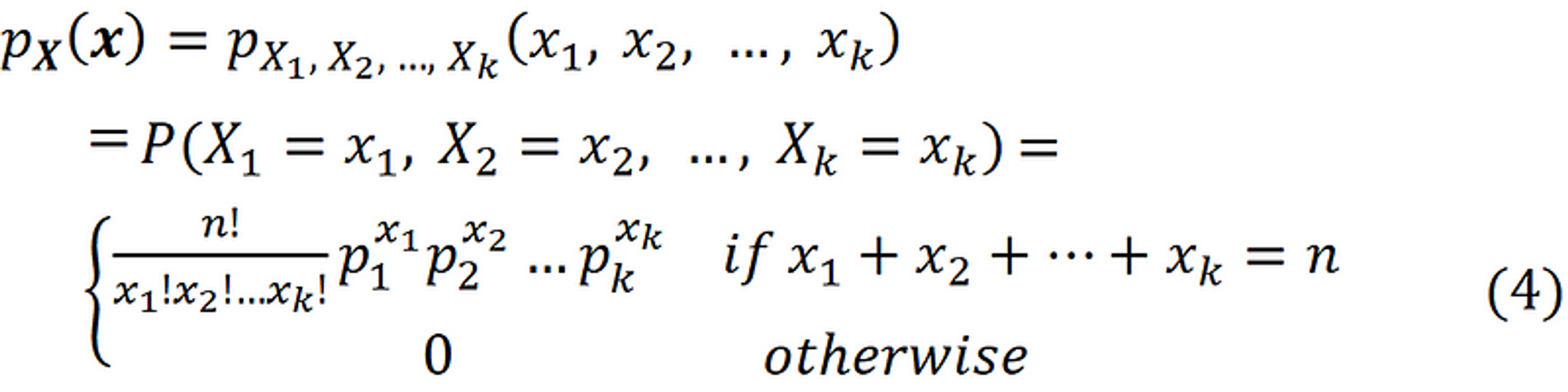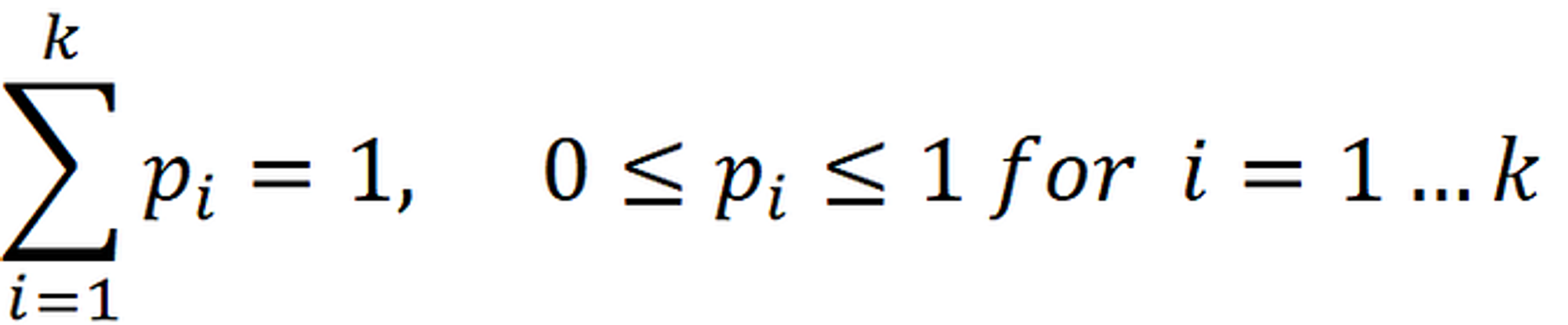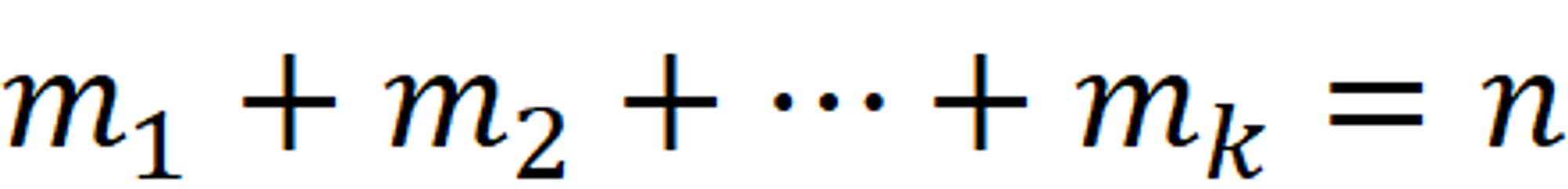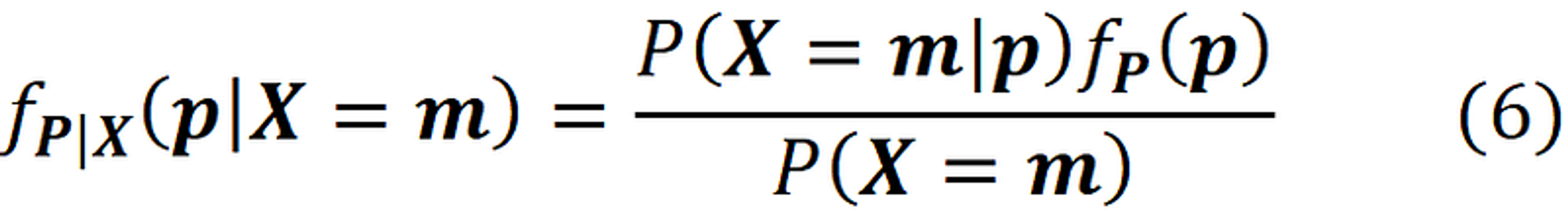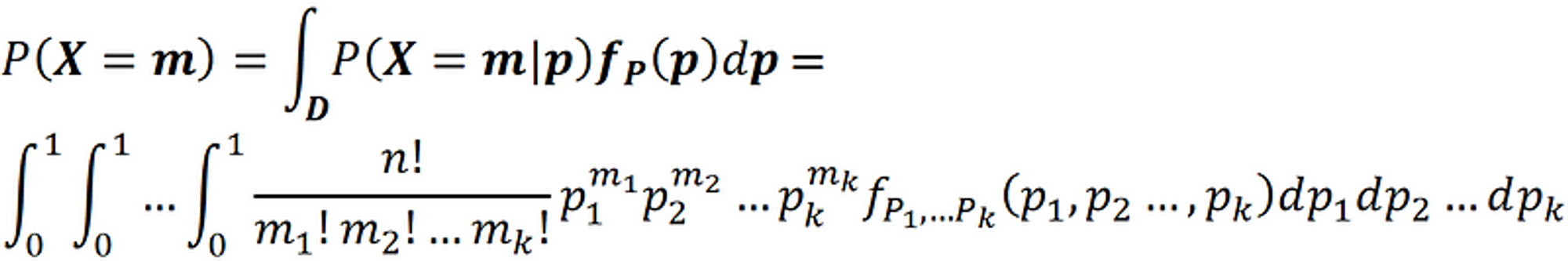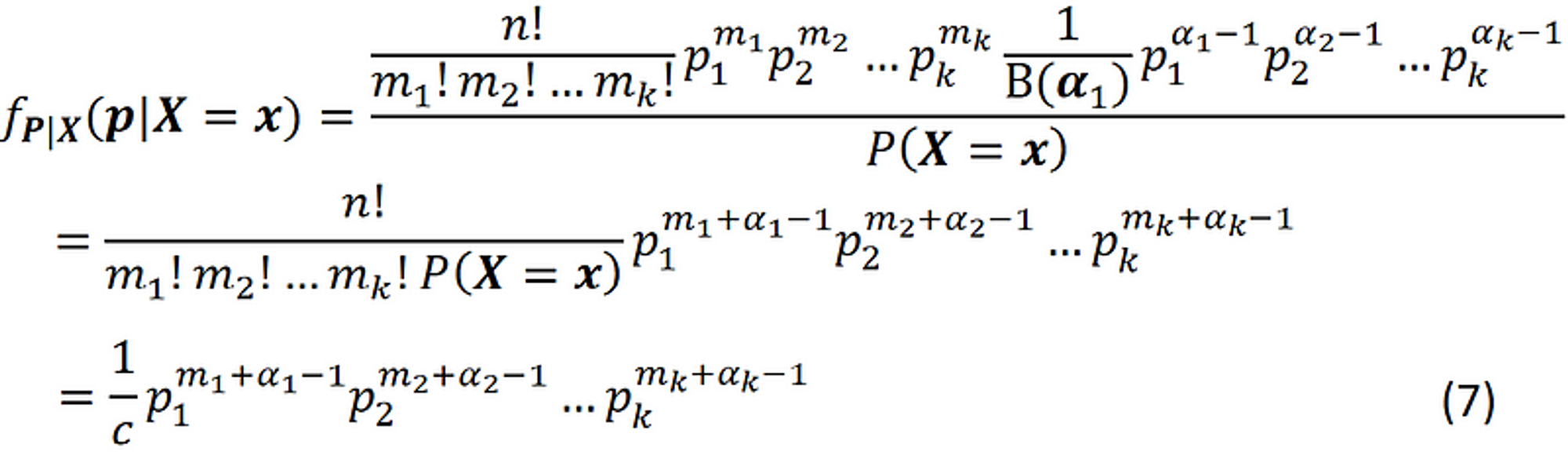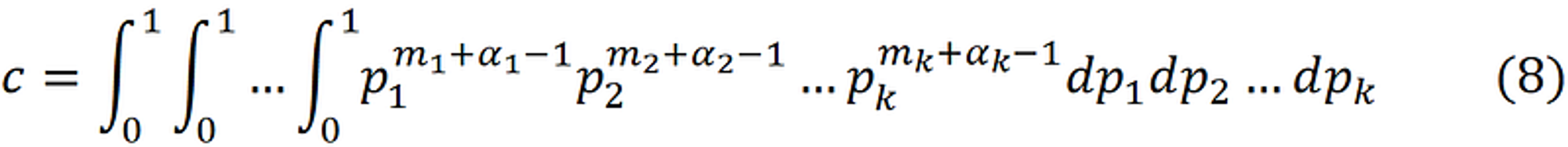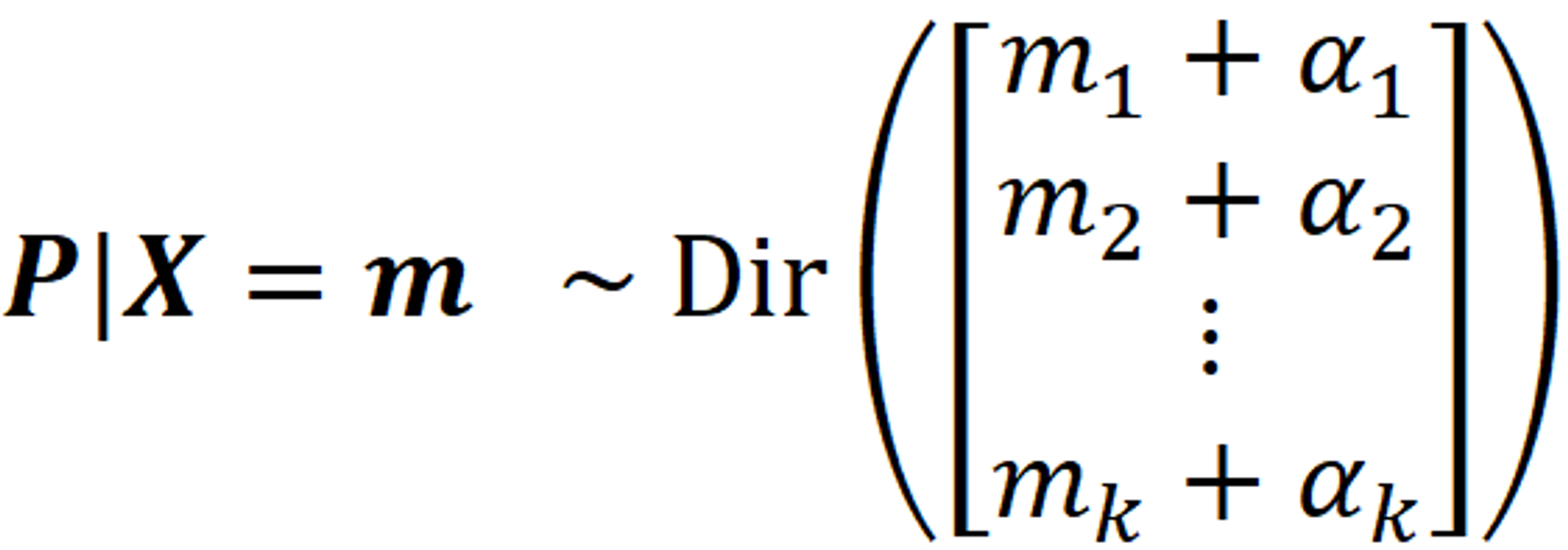Gama&Beta&Dirichlet
0. 前言
这篇 Blog 主要对几个分布进行总结, 以及对他们之间的关系进行梳理
1. Gamma Function
- 定义
记忆方法: 理解为用一个伽马刀, 对 $t$ 动了一刀, 于是指数为 $\alpha-1$, 动完刀需要扶着梯子 $-t$ 才能走下来。
- 性质
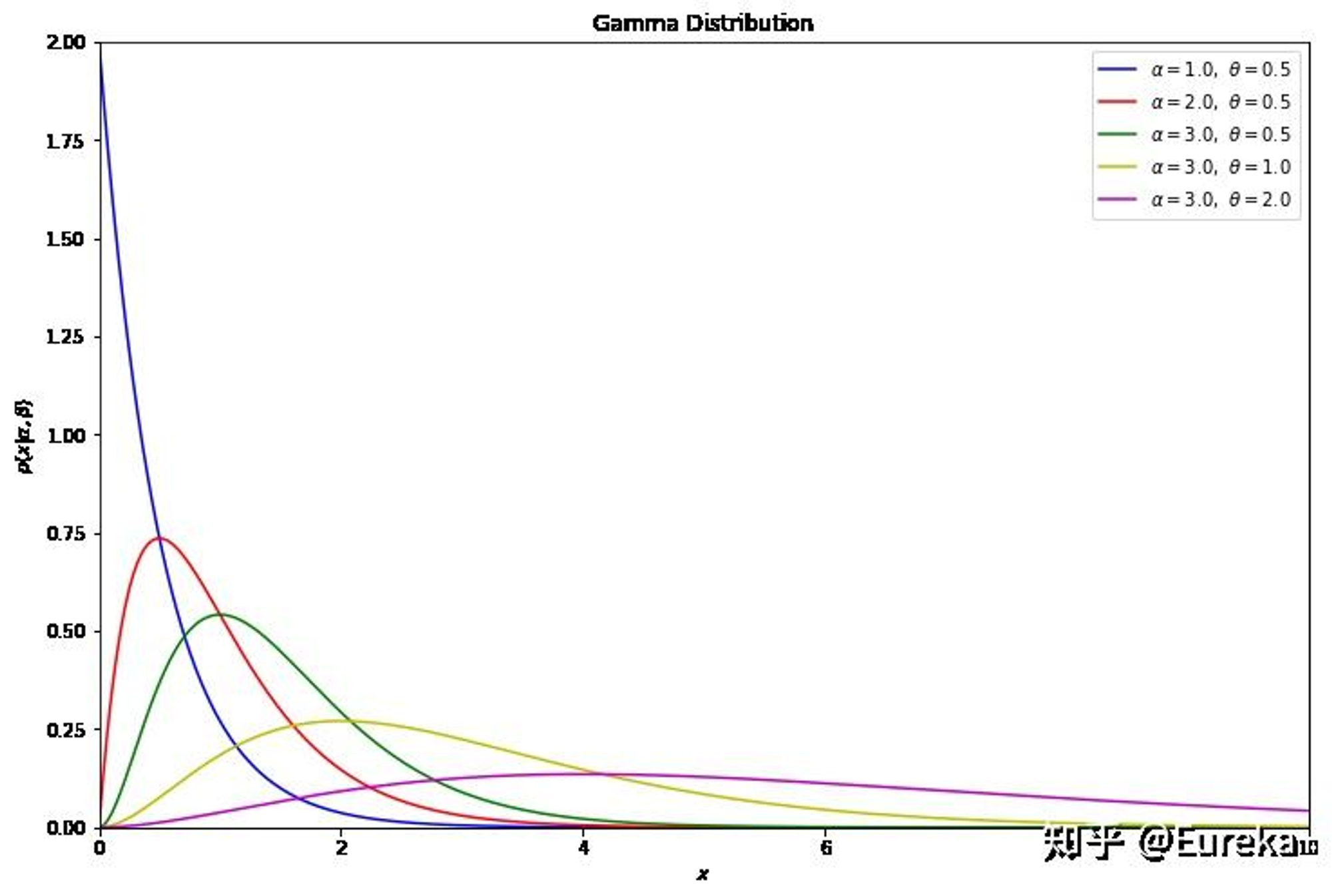
2. Gamma Distribution
对Gamma函数等式左右两端, 同时除以$\Gamma(\alpha)$, 则有
于是取积分中的函数作为概率密度, 就得到一个简单的Gamma分布的密度函数:
如果做一个变换 $t=\beta x$, 就得到Gamma分布的更一般形式:
其中 $\alpha$ 称为shape parameter, 主要决定了分布曲线的形状, 而 $\beta$ 称为rate parameter或inverse scale parameter( $\frac {1} {\beta}$ 称为scale parameter), 主要决定曲线有多陡。
3. Binomial Distribution
二项分布是 n 次独立的是/非试验中成功的次数的离散概率分布, 其中每次试验的成功概率为p.
p 是已知的 , 给定 p , 求解目标成功次数对应的概率, 通常使用 $C(m, n, p)$ 来计算.
参数p 本身就有一个分布, 如何预估 参数p 本身的分布 ? 参考下边的 Beta分布
4. Binomial Distribution 的另一个理解
假设向长度为1的桌子上扔一个红球(如上图), 它会落在0到1这个范围内, 设这个长度值为 x (就是上边定义中的p), 再向桌上扔一个白球, 那么这个白球落在红球左边的概率即为 x (或者p). 若总共扔了n个白球, 每次都是独立的, 假设落在红球左边的白球个数为k, 那么次数 k 在给定参数 x (或者p)的分布为:
可以看到, 结果就是二项分布. 在这个例子的基础上, 进一步的我们来看 , 如果不关注 概率 p , 我们来求解泛化下的 k次成功概率, 即 需要对 p 积分 (这里是对x积分)
这个比较难计算, 我们换个思路, P(K=k)就是想说总共n个白球, 1个红球随便放, 然后红球左边的白球个数为 k 的概率. 而 红球的位置是未知的
ok, 现在假设k=1, 换句说, 理解为总共n+1个球, 把第2个球涂为红色(左边就1个白色): $P = \frac {1} {n+1}$
ok, 现在假设k=2, 换句说, 理解为总共n+1个球, 把第3个球涂为红色(左边就2个白色): $P = \frac {1} {n+1}$
…
同理, 即得
5. Beta Function
在上边的式子基础上, 令 $k = \alpha - 1$ , $n - k = \beta - 1$ , 则 $n = \alpha + \beta - 2$ , 变量换为 $t$
则有
- 定义 $Beta$ 函数
根据之前 $Gama(\alpha)$ 函数的定义 , $Beta(\alpha, \beta)$ 可以表示为 :
6. Beta Distribution
其中 $Beta(\alpha, \beta)$ 起到归一化的作用
The Beta distribution is the conjugate prior for the Bernoulli, binomial, negative binomial and geometric distributions (seems like those are the distributions that involve success and failure) in Bayesian inference. see what’s means that “conjugate prior” ?
- 性质
$Beta$ 分布 与 之前的 Bernoulli 分布 (0 -1 分布) , Binomial 分布 (即二项分布 , $C(m, n, p)$ ) 构成共轭分布.
-
[1]
Binomial分布(二项分布 ) 理解为给定成功概率参数 $p$ 和实验次数 $n$ 的情况下, 成功 $k$ 次的概率分布. -
[2] Beta分布是在给定成功次数 $\alpha$ 和失败次数 $\beta$ (通常来自实验观察, $p$ 未知) 后 , 探究成功概率参数 $p$ 的分布 (即上述公式中的 x 的分布) . 看起来像是一种对偶的关系, 不过更多人叫他是共轭关系
7. Multinomial Distribution
- 定义
[1] 这里 p 是已知的 , 给定 p , 求解目标成功次数对应的概率. 对于此时参数p本身的分布 , 参考下方 Dirichlet Distribution
[2] 这里可以看到, Multinomial Distribution 其实可以理解为多维的 “二项分布” , 即 “多项分布”.
上述函数, 如果使用 $\Gamma$ 函数表示 :
8. Multinomial Distribution的另一种理解
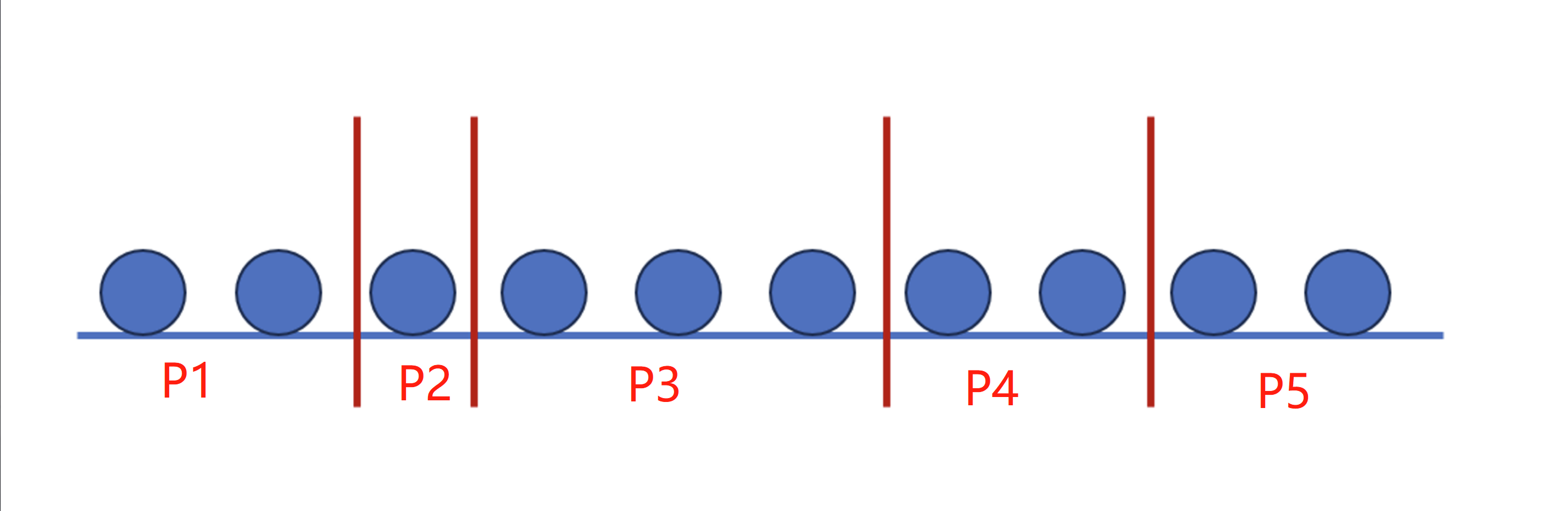
可以结合之前的小球案例, 多项分布 可以理解为如下案例
将 $n$ 个球 放到不同的箱子中, 每个箱子分到的小球的个数分别是 $x_1, x_2\ …\ x_n$ 的概率, 进一步转换 , 可以理解为把小球一字排开, 然后在中间放隔板(在哪里放隔板是根据一定概率$p_i$), 使得间隔内的球数目为 $x_1, x_2\ …\ x_n$ , 然后得到
\[f(x_1 , \ ... \ , x_k, n , p_1, p_2 \ ... \ p_n)\ = \ C*p_1^{x_1} * \ ... \ p_n^{x_n}\]前边的系数C, 我们可以这样理解, 因为我们关注的是每个箱子中小球的具体数量, 不关注箱子内小球的顺序 . 所以我们可以先假设是有顺序的, 然后再把顺序删除就能算得相应的小球放置情况的数量
- 假设有顺序, 那么首先 n 个小球全排列 : $n!$ (有顺序)
- 然后删除顺序, 只不过将这个过程分配给每个箱子内部实现 : 每个箱子内部除以 $x_i{!}$ 即可, 便得到上述结果
9. Dirichlet Distribution
- 定义
其中 $Beta(\alpha)$ 还是起到归一化的作用, 这里的 $x$ 就是参数 $p$ , 其中
同理, 使用 $\Gamma$ 函数 可得到 $Beta(\alpha)$ 的另一种表示
可以看到
Multinomial Distribution和Dirichlet Distribution的关系 类似Binomial Distribution和Beta Distribution的关系 . 这里Multinomial Distribution是给定各个|箱子|板子|老虎机|成功概率 $p$ , 然后去求解不同成功次数对 应的概率.而Dirichlet Distribution要做的是, 根据成功次数(或者已知成功次数) $\alpha$ 去探讨每个|箱子|板子|老虎机|成功概率, 或者可以说 把Beta Distribution和Dirichlet Distribution作为了成功概率的先验分布 .
- 性质
在老虎机场景下. 假设离散随机变量 $X$ (可以理解为每个Bandit成功的次数)
令各Bandit的成功概率为
那随机变量 $X$ 的分布为 (就是多项分布)
那参数 $p$ 的先验分布就是 Dirichlet Distribution
- 应用
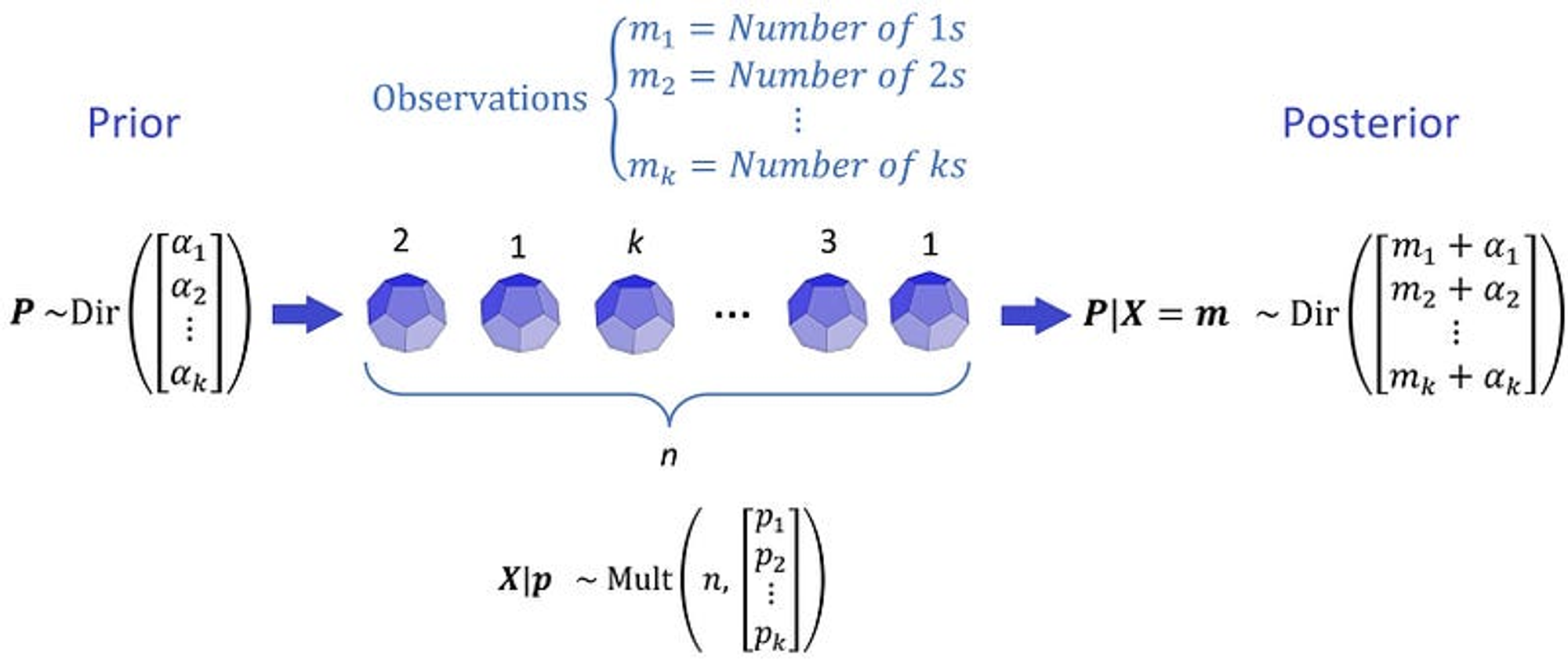
如下案例, 类似Bandit, 只不过使用筛子.
现在假设不知道每个 bandit 的成功概率, 就是说不知道骰子每个面朝上的概率, 我们要通过试验来得到这些概率, 那我们就会有以下内容:
其中,
相应的发生次数概率计算结果
那么根据实验结果来预估潜在的 $p$ (就是后验分布), 可以使用Bayes rule:
其中, 分母 $P(X=m)$
然后分子中的 $f_p(P)$ 就是上边的先验分布 Dirichlet Distribution , 整体带入即得
这里 c 取到归一化的作用:
可以看到, 潜在参数 $p$ 的后验分布仍然是 Dirichlet distribution:
既有
那么对于 每个Bandit或者筛子, 先初始化 Dirichlet distribution , 然后根据Bandit或者筛子的结果, 更新其相应的概率分布即可. 然后再根据当前的概率分布进行下一步采样(就是基于当前概率分布, 选择认为赢得概率更高的Bandit, 然后看结果, 循环更新分布).
当然这里就会涉及到采样, 即怎么快速高效的根据已有的分布采样? 这是另外的问题了…. 可以移步至Sampling-Method
Reference
[1] https://zhuanlan.zhihu.com/p/37976562