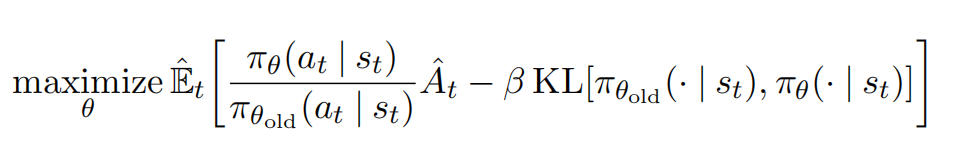Deep Reinforcement Learning Series

0. 前言

本篇 Blog 主要对强化学习的几个参数更新方法进行学习.

阅读前, 需要你 : 有高数基础知识, 线代基础知识, 统计学习基础知识, 当然还要有 ML和 DL 的知识背景.

1. 总览和相关概念

1.1 总览

source from David Silver’s RL Course

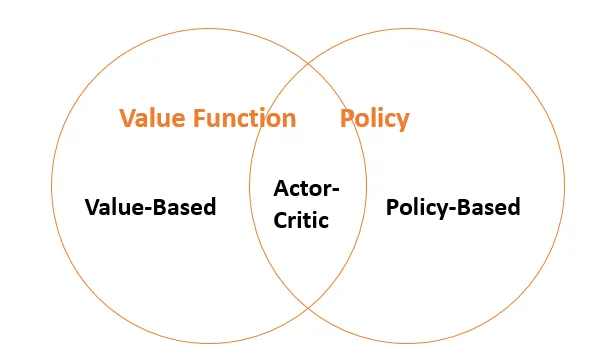
目前, 强化学习的方法基本上划分为 2 大类: policy based and value based.

• policy based 主要是通过学习一个 Actor, 在面对 state 的时候输出预估最优的 action.

• value based 则是想通过学习一个 critic, 来评估当前这个 state 下, 哪个 action 能够得到的分数最高, 进而实现选择 action.

当然这么说好像看起来没有什么区别, 后续我们会深入分析他们的区别和联系. 最后还有把 policy based and value based 结合起来的, 就是既有 Actor 也有 Critic.

1.2 概念

• observation

比如你打游戏, 这一帧画面就是一个 observation, 有时候也称为一个 state, 就是包含了当前系统的状态和所有信息.

• action

就是面对当前画面, 采取的措施, 看到敌人你是躲还是开枪?

• reward

基于当前 observation, 你采取了行动 action, 将得到奖励, 比如开枪干掉了对面, 得到 100 分.

• episode

这里拿飞机大战举例子, 从你进入游戏, 左右闪躲腾挪, 开枪击毁对面飞机,直到游戏结束, 这就叫一个 episode.

• trajectory

还是飞机大战, 从你进入游戏, 左右闪躲腾挪, 开枪击毁对面飞机, 直到游戏结束(假设T时间步), 在你这一个 episode 中, 你看到的所有画面帧, 所有的行动, 所有的奖励, 这样一个序列称为一个 trajectory:

\[\tau = { \underbrace{s_1,a_1,r_1}_{observation 1,\ action 1,\ reward 1 } \ ... \ s_T,a_T,r_T }\]

2. Policy Based

2.1 要做什么

前边提到 Policy Based 要训练一个 Actor. Actor 理解为就是一个 $model \ with \ parameter \ \theta$ , 给定当前的 observation $s_t$ , Actor 评估当前某个 action $a_t$ 的概率 : $p(a_t | s_t,\theta)$.

那怎么训练呢? 假设已经有一个 trajectory $\tau$, 这样的序列除了第一个 state 是初始化, 后续你遇到的每一个 state 都是 Actor 选择的 action 导致的, 因此只需要收集这样一批 trajectory, 每个 trajectory 我们都能收集到相应的奖励 $R(\tau)$, 我们希望这个 Actor 能够在平均的,期望上的奖励能够最大:

\[max \ \mathbb{E}_{\tau} [R(\tau)] = \sum_{\tau} R(\tau) p(\tau | \theta)\]

2.2 理论怎么做

2.2.1 计算 $p(\tau | \theta)$

\[\begin{align*} p(\tau | \theta) &= p(s_1) p(a_1|s_1,\theta)p(r_1,s_2|s_1,a_1)p(a_2|s_2,\theta)p(r_2,s_3|s_2,a_2)... \newline &= \underbrace{p(s_1)}_{crate \ by \ env\ } \prod_{t=1}^{T} \underbrace{p(a_t|s_t,\theta)}_{crate \ by \ actor\ }\underbrace{p(r_t,s_{t+1}|s_t,a_t)}_{\ crate \ by \ env} \end{align*}\]

2.2.1 计算梯度

通常我们利用梯度方向更新参数, 所以需要计算 $\mathbb{E}_{\tau} [R(\tau)]$ 关于 $\theta$ 的梯度:

\[\begin{align*} \nabla \tilde{R}_{\theta} &= \sum_{\tau} R(\tau) \nabla p_{\theta}(\tau) \newline &= \sum_{\tau} R(\tau) p_{\theta}(\tau) \nabla log \ p_{\theta}(\tau) \newline &= \mathbb{E}_{\tau} [R(\tau) \nabla log \ p_{\theta}(\tau) ] \newline & \approx \frac{1}{N} \sum_{n=1}^{N} R(\tau^n) \nabla log \ p_{\theta}(\tau^n) \end{align*}\]

这里, 对于任意 $\tau$ :

\[\begin{align*} \nabla log \ p_{\theta}(\tau) &= log \ p(s_1) + \sum_{t=1}^{T} [log \ p(a_t|s_t,\theta) + log \ p(r_t,s_{t+1}|s_t,a_t)] \end{align*}\]

上式中, $log \ p(s_1)$ 与 Actor 无关, $log \ p(r_t,s_{t+1}|s_t,a_t)$ ,也与 Actor 无关, 因此:

\[\begin{align*} \nabla log \ p_{\theta}(\tau) &= \sum_{t=1}^{T} \nabla log \ p(a_t|s_t,\theta) \end{align*}\]

于是:

\[\begin{align*} \nabla \tilde{R}_{\theta} &= \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T} R(\tau^n) \nabla log \ p(a_t^n|s_t^n,\theta) \end{align*}\]

写成期望的版本:

\[\begin{align*} \nabla \tilde{R}_{\theta} &= \mathbb{E}_{(s_t,a_t) \sim p_{\theta}} [R(\tau) \nabla log \ p(a_t |s_t,\theta)] \end{align*}\]

使用梯度提升更新 Actor 的参数:

\[\theta^{new} = \theta^{old} + \eta \nabla \tilde{R}_{\theta}\]

2.2.2 改进奖励计算方式

上边在建模 reward 的时候, 任何 action 的奖励都是正的, 这明显不合理, 因此可以加一个 baseline :

\[\begin{align*} \nabla \tilde{R}_{\theta} &= \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T} [R(\tau^n) - b] log \ p(a_t^n|s_t^n,\theta) \end{align*}\]

一般的, baseline b 可以取值为截至目前的平均 reward: $b \approx \mathbb{E}_{\tau} [R(\tau)] $.

此外, 上边式子可以理解为是对 $log \ p(a_t^n|s_t^n,\theta)$ 的一个 sum weight. 其中 $R(\tau^n) - b$ 表示的是, 在 state $s_t$ 时采取 action $a_t$ 时对后来获得的总奖励的影响是多大.

另外还可以从减少 variance 的角度来理解, 可移步至此(点击跳转)

在上边的公式中, 这个 weight 对每个时间步 t 都一样, 均为 $R(\tau^n) - b$. 直觉上, 当前时间步 t 采取的动作, 只能影响 时间步 t 之后的奖励或者状态等. 并且随着时间流逝, 时间步 t 采取的动作对后续的影响应该越来越小, 因此对 $R(\tau)$ 进行修改(忽略 b ):

\[R(\tau^n) = \sum_{t' = t}^{T_n} \gamma^{t'-t}r_{t'}^{n}\]

其中, $\gamma < 1$, baseline 也同步修改. 举个例子, 假设 $\gamma = 0.99, t = 3 , T = 5$:

\[R(\tau^n) = r_3 + 0.99*r_4 + 0.99^2*r_5\]

注意到, 此时 $R(\tau^n)$ 是想评估当前 actor 基于当前 state $s_t$ 和 action $a_t$ 的分数, 不妨记为 $Q^{\pi}(s_t,a_t)$, 而 $b$ 可以理解为度量面对当前 state $s_t$ (不与 action 有关), 这个 actor 平均能够取得的分数, 不妨记为 $V^{\pi}(s_t)$, 那如果把 $Q^{\pi}(s_t,a_t) - V^{\pi}(s_t)$ 记为 $A^{\theta}(s_t,a_t)$, 其实这就是 Value Based 方法 (也就是一个 critic). 二者结合, 就是 Actor - Critic, 我们后续会讨论. 此时, 之前的期望公式就可以写为:

\[\begin{align*} \nabla \tilde{R}_{\theta} &= \mathbb{E}_{(s_t,a_t) \sim p_{\theta}} [A^{\theta}(s_t,a_t) \nabla log \ p(a_t |s_t,\theta)] \end{align*}\]

2.3 实际怎么做

前边的更新策略有个大问题就是, 我们要收集数据, 这个需要一轮一轮的玩下去才能收集到这些信息. 而且更新的这个 Actor 和 环境进行交互的 Actor 是同一个, 这就导致收集一批数据, 更新 Actor 之后, 整个过程就得停下来, 用新的 Actor 再次和环境进行交互 (这个过程称为 Online-policy). 这样就会很慢, 我们想着能不能让当前的 Actor 借助别人的力量, 使用别人的历史数据去更新?(这个过程称为 Offline-policy)

2.3.1 Importance Sampling

首先介绍一个 trick, 假设我们要计算 $\mathbb{E}_{x \sim p} [f(x)] $ , 但是 $p(x)$ 也许不好计算, 不好得到, 但是我们有一个分布 $q(x)$, 计算很容易, 也很容易积分:

\[\begin{align*} \mathbb{E}_{x \sim p} [f(x)] &= \int f(x)p(x) \ d(x) \newline &= \int f(x)p(x) \frac{q(x)}{q(x)} \ d(x) \newline &= \int f(x) \frac{p(x)}{q(x)} q(x) \ d(x) \newline &= \mathbb{E}_{x \sim q} [f(x)\frac{p(x)}{q(x)}] \end{align*}\]

可以看到, 本来是从 $p(x)$ 抽取数据, 现在做到从 $q(x)$ 抽取数据, 并且期望还不变. 但是需要注意的是, 他们的方差是不一样的.

首先:

\[\begin{align*} Var_{x \sim p} [f(x)] &= \mathbb{E}_{x \sim p} [f(x)^2] - (\mathbb{E}_{x \sim p} [f(x)] ) ^2 \end{align*}\]

而:

\[\begin{align*} Var_{x \sim q} [f(x) \frac{p(x)}{q(x)} ] &= \mathbb{E}_{x \sim q} [(f(x)\frac{p(x)}{q(x)})^2] - (\mathbb{E}_{x \sim q} [f(x)\frac{p(x)}{q(x)}] ) ^2 \newline &= \int f(x)^2 \frac {p(x) p(x)} {q(x) q(x)} q(x)\ d(x) - (\int q(x) f(x) \frac {p(x)}{q(x)} \ d(x)) ^ 2 \newline &= \mathbb{E}_{x \sim p} [f(x)^2\frac {p(x)}{q(x)}] - (\mathbb{E}_{x \sim p} [f(x)] ) ^2 \newline & \neq \mathbb{E}_{x \sim p} [f(x)^2] - (\mathbb{E}_{x \sim p} [f(x)] ) ^2 \end{align*}\]

二者方差差一点, 因此要求 $p(x)$ 和 $q(x)$ 不要差太多.

2.3.2 off - policy

off-policy 就是利用上边的 importance sampling, 使用另外一个 policy ${\theta_{old}}$ 的 {( $s_t,a_t$ )} 去更新 policy ${\theta}$. 于是,

\[\begin{align*} \nabla \tilde{R}_{\theta} &= \mathbb{E}_{\tau} [R(\tau) \nabla log \ p_{\theta}(\tau) ] \newline &= \mathbb{E}_{\tau \sim p_{\theta_{old}}(\tau)} [\frac { p_{\theta}(\tau)} { p_{\theta_{old}}(\tau)} R(\tau) \nabla log \ p_{\theta}(\tau) ] \newline &= \mathbb{E}_{(s_t,a_t) \sim p_{\theta_{old}}} [\frac { p_{\theta}(a_t , s_t)} { p_{\theta_{old}}(a_t , s_t)} R(\tau) \nabla log \ p_{\theta}(\tau) ] \newline &= \mathbb{E}_{(s_t,a_t) \sim p_{\theta_{old}}} [\frac { p_{\theta}(a_t | s_t)p_{\theta}(s_t)} { p_{\theta_{old}}(a_t | s_t)p_{\theta_{old}}(s_t)} R(\tau) \nabla log \ p_{\theta}(\tau) ] \ (p_{\theta}(s_t) \approx p_{\theta_{old}}(s_t)) \newline &= \mathbb{E}_{(s_t,a_t) \sim p_{\theta_{old}}} [\frac { p_{\theta}(a_t | s_t)} { p_{\theta_{old}}(a_t | s_t)} R(\tau) \nabla log \ p_{\theta}(\tau) ] \end{align*}\]

上式 $p_{\theta}(s_t) \approx p_{\theta_{old}}(s_t)$ 是我们进行的假设, 假设环境在第 t 步出现的状态和 Actor 无关( 看起来不太合适, 这个也是没办法的办法 ). 此外 policy ${\theta_{old}}$ 是固定的, 用来和环境交互, policy ${\theta}$ 是我们要更新的. 更新一段时间后, 我们可以执行 $\theta_{old} <– \theta$ 以防二者差距太大.

这样, 反推得到:

\[\begin{align*} \tilde{R}_{\theta}^{\theta_{old}} &= \mathbb{E}_{(s_t,a_t) \sim p_{\theta_{old}}} [\frac { p_{\theta}(a_t | s_t)} { p_{\theta_{old}}(a_t | s_t)} R(\tau)] \end{align*}\]

如果使用 Actor - Critic 的方式评估 $R(\tau)$,之前的期望公式就可以写为:

\[\begin{align*} \nabla \tilde{R}_{\theta} &= \mathbb{E}_{(s_t,a_t) \sim p_{\theta_{old}}} [\frac { p_{\theta}(a_t | s_t)} { p_{\theta_{old}}(a_t | s_t)} A^{\theta_{old}}(s_t,a_t) \nabla log \ p_{\theta}(\tau) ] \end{align*}\]

反推得到

\[\begin{align*} \tilde{R}_{\theta}^{\theta_{old}} &= \mathbb{E}_{(s_t,a_t) \sim p_{\theta_{old}}} [\frac { p_{\theta}(a_t | s_t)} { p_{\theta_{old}}(a_t | s_t)} A^{\theta_{old}}(s_t,a_t)] \end{align*}\]

2.4 PPO

在上边的基础上, 我们来看经典算法 PPO. PPO 其实就是在上边的基础上, 加了一个 KL 散度(什么是 KL 散度?), 这是因为我们要尽量保证 $\theta_{old} \approx \theta$. 这里直接贴出原始 paper 的公式, 现在一目了然:

这里 KL ( $\theta_{old}$ , $\theta$) 实际上就是让二者的输出, 计算一下离散的 KL 散度值作为代替. 不过作者又给了一个更加简单粗暴的实现: 如果二者差距确实大,直接 clip 一下就完事了:

这样就把 $\frac { p_{\theta}(a_t | s_t)} { p_{\theta_{old}}(a_t | s_t)}$ 限制到了 $(1- \epsilon , 1 + \epsilon)$.

3. Value Based

3.1 概念

[1] Value Based 的方法目标就是训练一个 critic, 也可以叫一个 function, 功能就是给定一个 state (或者以及一个 action), critic 能够评估当前这个 Actor(policy : $\pi$) 最后能取得多少分数(相对的,平均).

不妨记, $V^{\pi}(s)$ 表示给定一个 state s, critic 给出的基于当前 state, 该 policy 能得到的分数(平均).

\[V^{\pi}(s) = \mathbb{E}_{\pi}[R_t | S_t = s] = \mathbb{E}_{\pi}[\sum_{k = 0}^{\infty} \gamma^{k}R_{t+k} | S_t = s]\]

如果对于任意的 state s, 如果 $V^{\pi’}(s) >= V^{\pi}(s) $ 恒成立, 则称 $\pi’$ better than $\pi$. 于是这样, 我们整个系统中, 最好的那个 $\pi$ 记为 $\pi_{\ast}$ . 并将 $\pi_{\ast}$ 对应的 V 记为 $V^{\ast}(s)$. 即

\[V^{\ast}(s) = \mathop{\max}\limits_{\pi} \ V^{\pi}(s)\]

[2] $Q^{\pi}(s,a)$ 表示给定一个 state s, 然后 Actor 采取一个 action a, critic 给出的基于当前 state 和 action, 该 Actor 能最后得到的分数(平均).

\[Q^{\pi}(s,a) = \mathbb{E}_{\pi}[R_t | S_t = s , A_t = a ] = \mathbb{E}_{\pi}[\sum_{k = 0}^{\infty} \gamma^{k}R_{t+k} | S_t = s , A_t = a ]\]

同理, $\pi_{\ast}$ 在每个 state 上采取的 action a, 将 Q 值是最大记为如下形式:

\[Q^{\ast}(s,a) = \mathop{\max}\limits_{\pi} \ Q^{\pi}(s,a)\]

对于 $V^{\pi}(s)$ 和 $Q^{\pi}(s,a)$, 二者有以下关系:

\[Q^{\pi}(s,a) = \mathbb{E}_{\pi}[r_t + \gamma V^{\pi}(s_{t+1})| S_t = s , A_t = a ]\]

当然, 对于最优的 value,那么会有如下的式子成立:

\[Q^{\ast}(s,a) = \mathbb{E}_{\pi}[r_t + \gamma V^{\ast}(s_{t+1})| S_t = s , A_t = a ]\]

3.2 Bellman equation

3.2.1 Bellman equation for $V^{\pi}(s)$

\[\begin{align*} V^{\pi}(s) &= \mathbb{E}_{\pi}[R_t | S_t = s] \newline &= \mathbb{E}_{\pi}[\sum_{k = 0}^{\infty} \gamma^{k}R_{t+k} | S_t = s] \newline &= \mathbb{E}_{\pi}[r_t + \sum_{k = 1}^{\infty} \gamma^{k}R_{t+k} | S_t = s] \newline &= \sum_{a} \pi(a | s) \sum_{s'} \sum_{r} p(s', r | s, a) [r + \gamma \mathbb{E}_{\pi}[\sum_{k = 0}^{\infty} \gamma^{k}R_{t+k+1} | S_{t+1} = s']] \newline &= \sum_{a} \pi(a | s) \sum_{s', \ r} p(s', r | s, a) [r + \gamma V^{\pi}(s')] \end{align*}\]

上边这个式子称为 $V^{\pi}(s)$ 的 Bellman equation, 它揭示了当前 $\text{state s}$ 下的 $V^{\pi}$ 与下一时刻的 $\text{state s’}$ 的 $V^{\pi}$ 之间的关系.

3.2.2 Bellman optimality equation for $V^{\pi}(s)$

从定义上我们有:

\[\begin{align*} V^{\ast}(s) &= \mathop{\max}\limits_{a} \ Q^{\pi_{\ast}}(s,a) \newline &= \mathop{\max}\limits_{a} \ \mathbb{E}_{\pi_{\ast}}[R_t | S_t = s, A_t = a] \newline &= \mathop{\max}\limits_{a} \ \mathbb{E}_{\pi_{\ast}}[\sum_{k = 0}^{\infty} \gamma^{k}R_{t+k} | S_t = s, A_t = a] \newline &= \mathop{\max}\limits_{a} \ \mathbb{E}_{\pi_{\ast}}[r_t + \gamma \sum_{k = 0}^{\infty} \gamma^{k}R_{t+k+1} | S_t = s, A_t = a] \newline &= \mathop{\max}\limits_{a} \ \mathbb{E}_{\pi_{\ast}}[r_t + \gamma V^{\ast}(s_{t+1})| S_t = s, A_t = a] \newline &= \mathop{\max}\limits_{a \in A(S)} \sum_{s',\ r } p(s', r | s, a)[r_t + \gamma V^{\ast}(s')] \end{align*}\]

上式称为 Bellman optimality equation for $V^{\pi}(s)$

3.2.3 Bellman optimality equation for $Q^{\pi}(s,a)$

按定义我们有:

\[\begin{align*} Q^{\ast}(s,a) &= \mathbb{E}_{\pi}[r_t + \gamma V^{\ast}(s_{t+1})| S_t = s , A_t = a ] \newline &= \mathbb{E}_{\pi}[r_t + \gamma \mathop{\max}\limits_{a'} Q^{\ast}(s_{t+1},a') | S_t = s , A_t = a ] \newline &= \sum_{s',\ r } p(s', r | s, a)[r_t + \gamma Q^{\ast}(s',a'))] \end{align*}\]

上式称为 Bellman optimality equation for $Q^{\pi}(s,a)$

3.3 Dynamic Programming Based

3.3.1 Policy Evaluation

动态规划的思想就很直观, 直接根据我们之前的 Bellman equation 迭代就行了, 因为 Bellman equation 描述的就是 $\pi_{\ast}$ 本身的性质. 更新迭代公式如下:

\[\begin{align*} V^{\pi}(s) \Leftarrow \sum_{a} \pi(a | s) \sum_{s', \ r} p(s', r | s, a) [r + \gamma V^{\pi}(s')] \end{align*}\]

上述迭代过程称为 iterative policy evaluation. 此外, 也可以使用 Bellman equation for $Q^{\pi}(s,a)$ 做迭代, 就是直接对 $Q^{\pi}(s,a)$ 迭代. 这个称为 Q-policy Iteration.

3.3.2 Policy Improvement

我们的目是找一个 policy, 能够面对不同的 state 采取一个action. 已知

\[\begin{align*} Q^{\pi}(s,a) &= \mathbb{E}_{\pi}[r_t + \gamma V^{\pi}(s_{t+1})| S_t = s , A_t = a ] \newline &= \sum_{s', \ r} p(s', r | s, a) [r + \gamma V^{\pi}(s')] \end{align*}\]

现在我们让 $Q^{\pi}(s,a)$ 最大, 这会得到一个相应的 action $a^{\ast}$ , 如果我们让另外一个 $\pi’$ 每次都能让以下式子成立:

\[\pi'(s) = a^{\ast}\]

这就意味着, 这个 $\pi’$ 每次都能采取最优的 action. 从而总是有:

\[V^{\pi'}(s) >= V^{\pi}(s)\]

于是:

\[\begin{align*} \pi'(s) &= \mathop{\arg\max}\limits_{a} \ Q^{\pi}(s,a) \newline &= \mathop{\arg\max}\limits_{a} \ \mathbb{E}_{\pi}[r_t + \gamma V^{\pi}(s_{t+1})| S_t = s , A_t = a ] \newline &= \mathop{\arg\max}\limits_{a} \ \sum_{s', \ r} p(s', r | s, a) [r + \gamma V^{\pi}(s')] \end{align*}\]

上述过程称为 Policy Improvement. 现在, 如果更新后的 policy 和原始的 policy 一样, 即 $V^{\pi} = V^{\pi’}$, 于是:

\[\begin{align*} V^{\pi'}(s) &= \mathop{\max}\limits_{a} \ Q^{\pi}(s,a) \newline &= \mathop{\max}\limits_{a} \ \mathbb{E}_{\pi}[r_t + \gamma V^{\pi}(s_{t+1})| S_t = s , A_t = a ] \newline &= \mathop{\max}\limits_{a} \ \sum_{s', \ r} p(s', r | s, a) [r + \gamma V^{\pi}(s')] \newline &= \mathop{\max}\limits_{a} \ \sum_{s', \ r} p(s', r | s, a) [r + \gamma V^{\pi'}(s')] \end{align*}\]

可以看到, 这就是 3.2.2 的 Bellman optimality equation for $V^{\pi}(s)$. 换句话说, 此时的 $\pi’ = \pi$ 就是最优的 $\pi$.

3.3.3 Policy Iteration

source from refer¹

我们使用 Policy Evaluation 去迭代 $V^{\pi}(s)$, 实现让 $V^{\pi}(s)$ 预估的更加准确.

然后, 我们使用 Policy Improvement 去找到一个更好的 $\pi$. 上述过程称为 Policy Iteration.

这个过程 Policy Evaluation 和 Policy Improvement 是交替循环的, 如下:

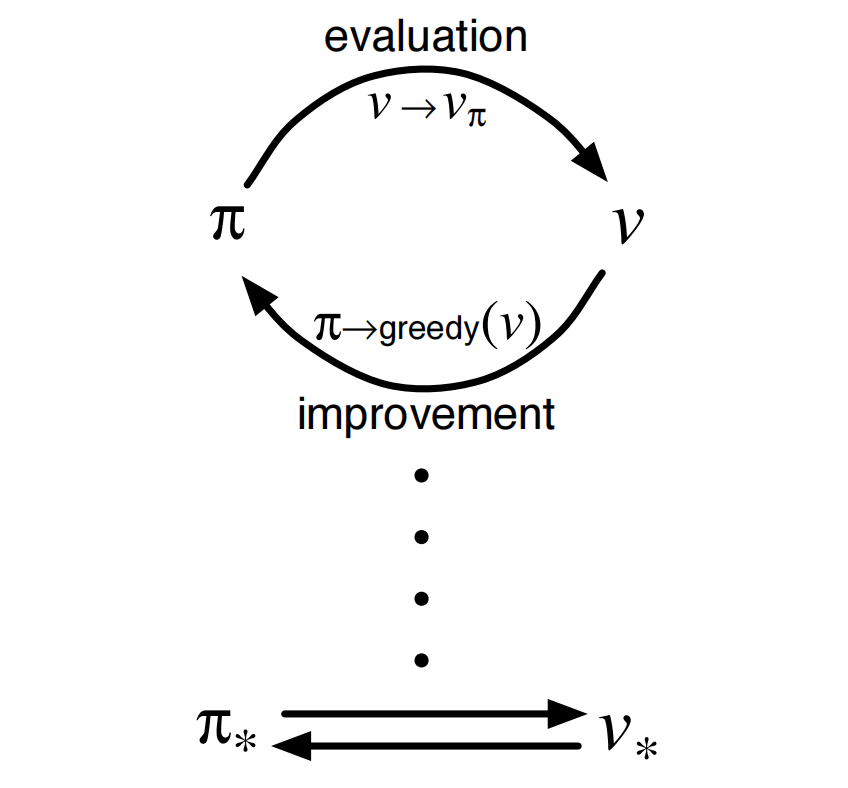source from refer¹

后续, 多个方法思路都是类似的, 上述循环过程称为 Generalized Policy Iteration.

3.3.4 Value Iteration

Policy Iteration 有 2 个步骤, 首先要让 V 预估准确, 然后再使用 Policy Improvement, 步骤比较繁琐, Value Iteration 的思想是, 直接从 Bellman optimality equation for $V^{\pi}(s)$ 入手 :

\[\begin{align*} V^{\ast}(s) &= \mathop{\max}\limits_{a \in A(S)} \sum_{s',\ r } p(s', r | s, a)[r_t + \gamma V^{\ast}(s')] \end{align*}\]

上述式子描述的是, 最优的 $\pi_{\ast}$ 能够满足的式子, 于是我们直接使用这个式子进行迭代:

\[\begin{align*} V(s) &= \mathop{\max}\limits_{a \in A(S)} \sum_{s',\ r } p(s', r | s, a)[r_t + \gamma V(s')] \end{align*}\]

当上式迭代收敛后, 得到的一个预估准确的 V function, 并且 $V(s)$ 的结果就是最优的 $\pi_{\ast}$ 对应的 V 值. 算法如下:

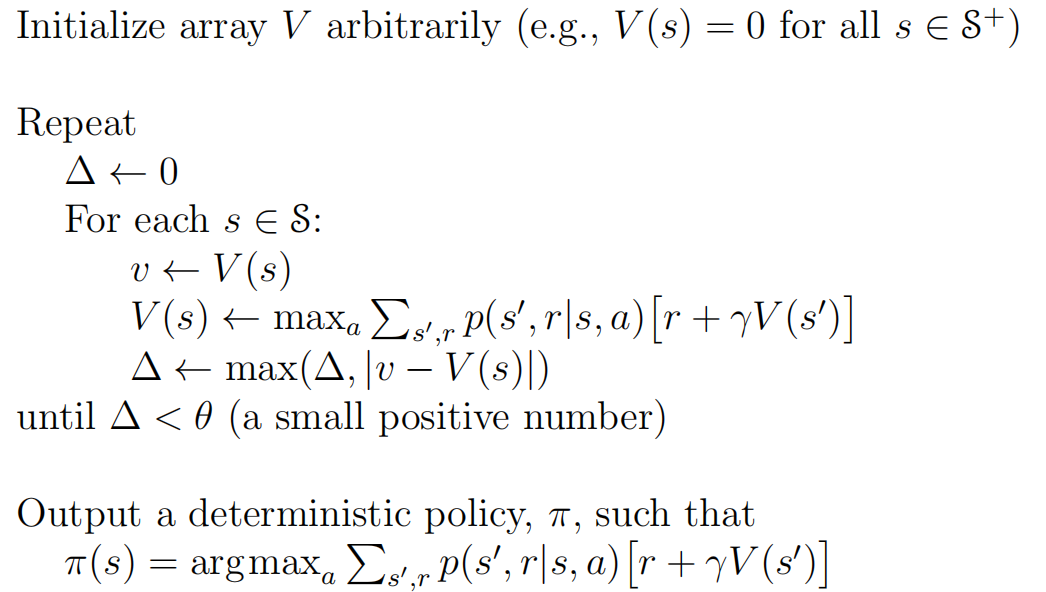source from refer¹

3.3.5 DP 方法总结

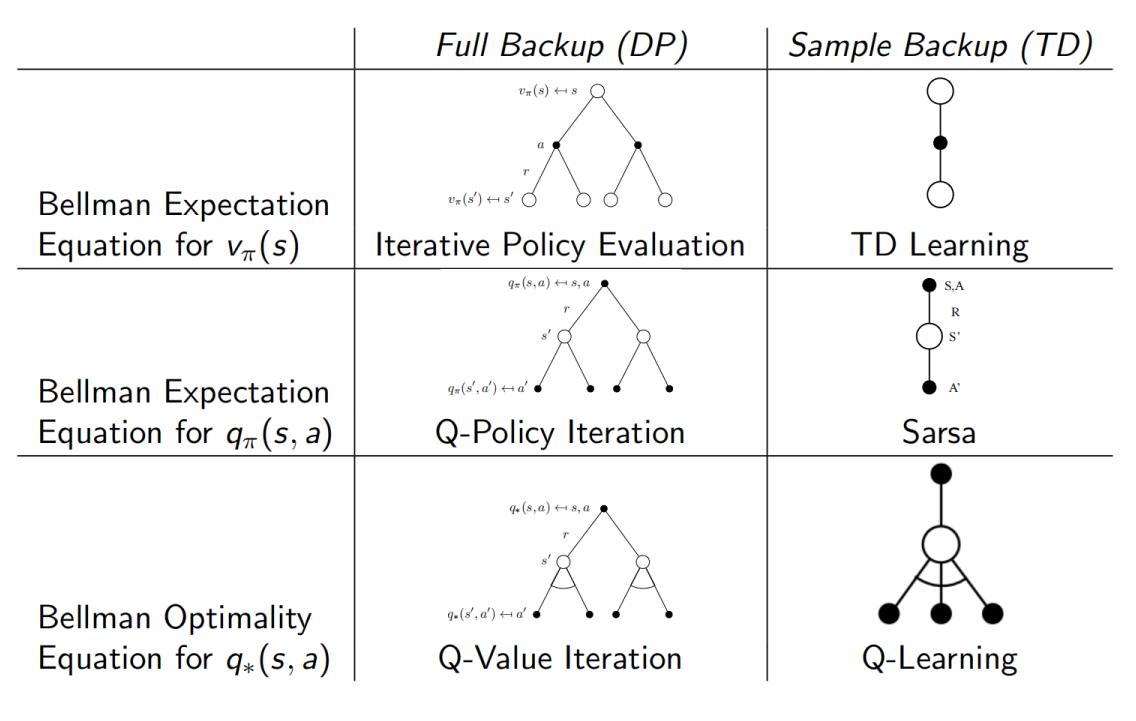
DP 方法总体思路为迭代方法, 主要基于 Bellman equation 进行迭代更新. 它基于当前状态, 观察所有可能的下一步来更新. 如图所示:

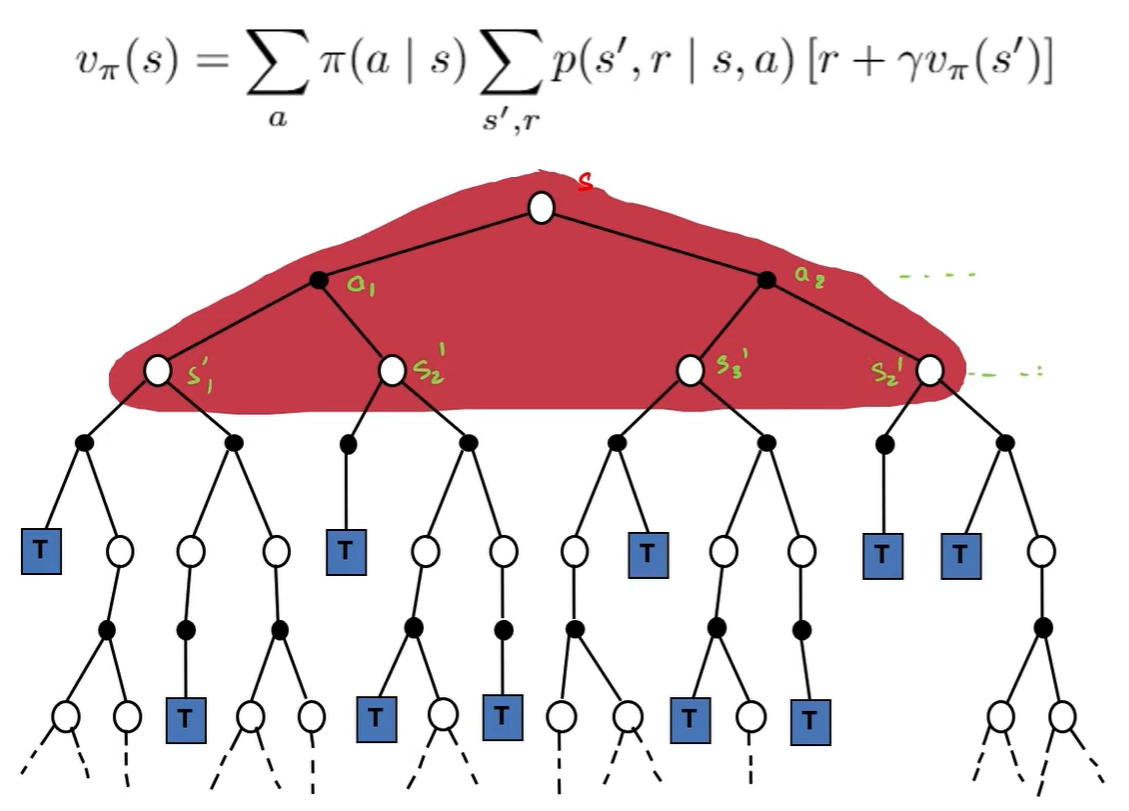source from refer²

3.4 Monte-Carlo based

3.4.1 state value based

Monte-Carlo 方法就很质朴, 直接基于当前 state, 然后你玩游戏直到结束, 记录分数, 最后求和得到累计奖励 $R$, 然后 minimize 二者的差距:

\[minimize \ V^{\pi}(s) \leftrightarrow R\]

具体的, 对于某个具体的 state $s$, 收集一批以 s 为起点的 trajectory, 最后计算 reward 的均值作为 $V^{\pi}(s)$:

source from refer¹

思想如图所示:

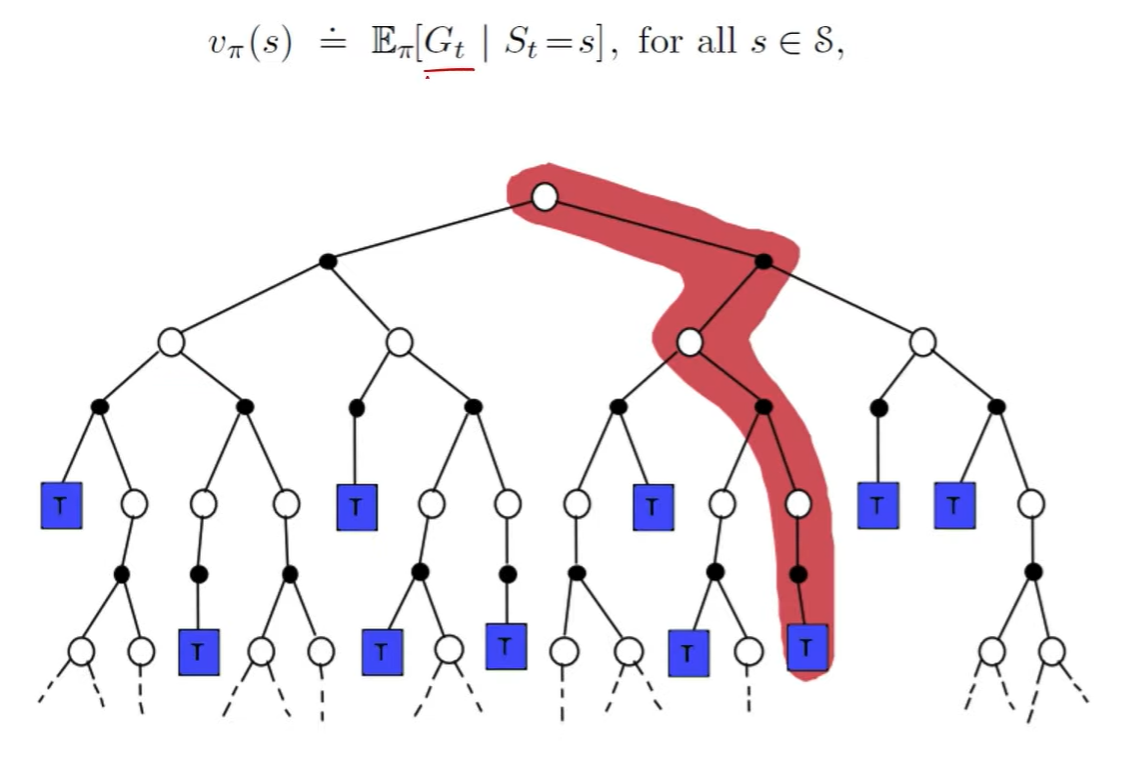source from refer²

3.4.2 state action value based

但是 state value based 可能比较困难, 因为要预估当前 state 下, 所有 action 的结果. 如果直接预估当前 state 下, 采取一个 action 之后的值可能好一点. 具体的, 收集一批以 state s , action a 为起点的 trajectory , 最后计算 reward 的均值作为 $Q^{\pi}(s,a)$:

source from refer¹

上述过程也是一个 cycle, 我们使用 Monte-Carlo 方法得到一个预估准确的 Q function, 然后使用这个 Q function 去让 $\pi(s) = \mathop{\arg\max}\limits_{a} \ Q^{\pi}(s,a) $ 实现 improvement 的操作. 这种取 max 的操作也叫做 $greedy$, 考虑到 Exploration/Exploitation trade-off , 如果每次都取 max, 会抑制后续的 exploration. 因此引入 $\epsilon - greedy$, 算法如下:

source from refer¹

3.5 Temporal-difference based

3.5.1 迭代公式

回顾 $V^{\pi}(s)$ 的定义: 计算 $\pi$ 面对当前 state s 能够获得的奖励, 记 $N_{a}^{k}(s)$ 表示基于当前 state 采样的 action 数目.

\[\begin{align*} V_{k}^{\pi}(s) &= \mathbb{E}_{\pi}[R_t | S_t = s] \newline &= \frac {1} {N_{a}^{k}(s)} (R_1 + R_2 + ... + R_{N_{a}^{k}(s)}) \ \ (采样) \newline &= \frac {1} {N_{a}^{k}(s)} ( R_{N_{a}^{k}(s)} + \sum_{i}^{N_{a}^{k}(s) - 1 } R_i ) \newline &= \frac {1} {N_{a}^{k}(s)} ( R_{N_{a}^{k}(s)} + (N_{a}^{k}(s)-1) V_{k -1 }^{\pi}(s) + V_{k -1 }^{\pi}(s) - V_{k -1 }^{\pi}(s)) \newline &= \frac {1} {N_{a}^{k}(s)} ( R_{N_{a}^{k}(s)} + N_{a}^{k}(s) V_{k -1 }^{\pi}(s) - V_{k -1 }^{\pi}(s)) \newline &= V_{k -1 }^{\pi}(s) + \frac {1} {N_{a}^{k}(s)} ( R_{N_{a}^{k}(s)} - V_{k -1 }^{\pi}(s)) \newline \end{align*}\]

抽象一下, 可以表示为下边的迭代公式:

\[\text{NewEstimate ← OldEstimate + StepSize [Target − OldEstimate]}\]

$V_{k -1 }^{\pi}(s)$ 告诉我们当前的预估, $R_{N_{a}^{k}(s)}$ 是真实看到的结果, $R_{N_{a}^{k}(s)} - V_{k -1 }^{\pi}(s)$ 告诉我们应该向实际看到的 reward 方向走, 这很像智能优化中的粒子群算法(关于该算法可以看我的视频讲解).

3.5.2 TD-Prediction

假设我们的 critic 是准确的, 应该有:

\[V^{\pi}(s_t) = \gamma V^{\pi}(s_{t+1}) + r_t\]

易知:

\[V^{\pi}(s_t) = (1 - \alpha) V^{\pi}(s_t) + \alpha V^{\pi}(s_t)\]

从而:

\[\begin{align*} V^{\pi}(s_t) &= (1 - \alpha) V^{\pi}(s_t) + \alpha ( \gamma V^{\pi}(s_{t+1}) + r_t) \newline &= V^{\pi}(s_t) - \alpha V^{\pi}(s_t) + \alpha ( \gamma V^{\pi}(s_{t+1}) + r_t) \newline &= V^{\pi}(s_t) + \alpha ( \gamma V^{\pi}(s_{t+1}) + r_t - V^{\pi}(s_t)) \end{align*}\]

上式中, $\gamma V^{\pi}(s_{t+1}) + r_t $ 描述的是向后预估一个 state $s_{t+1}$ 的 value. 然后再回过头来, 结合当前的预估值看预估的准不准, $\gamma V^{\pi}(s_{t+1}) + r_t - V^{\pi}(s_t)$ 也称为 temporal difference error (TD-error).

那如果 $V^{\pi}(s)$ 不准确, 我们可以使用 $\gamma V^{\pi}(s_{t+1}) + r_t$ 来纠正 $V^{\pi}$(因为 $r_t$ 至少是确定的).

于是,可以使用如下迭代公式更新 $V^{\pi}(s)$ :

\[\begin{align*} V^{\pi}(s_t) \leftarrow V^{\pi}(s_t) + \alpha ( \gamma V^{\pi}(s_{t+1}) + r_t - V^{\pi}(s_t)) \end{align*}\]

前边的 Monte-Carlo based 也可以写作如下式子:

\[\begin{align*} V^{\pi}(s_t) \leftarrow V^{\pi}(s_t) + \alpha ( R_t - V^{\pi}(s_t)) \end{align*}\]

所以 Monte-Carlo based 就是直接用真实的、整个 trajectory 的 reward 与 $V^{\pi}(s)$ 做比较, 而 Temporal-difference based 则是向后玩一步或者多步, 剩余的使用 $V^{\pi}$ 进行预估.

当然, 由于现在大家都是 neural network , 因此也可以直接使用梯度下降 minimize 以下差异³:

\[minimize \ V^{\pi}(s_t) - \gamma V^{\pi}(s_{t+1}) \leftrightarrow r_t\]

不过需要注意的是, MC 方法和 TD 方法有时候预估出来的结果可能不一样: source from refer³

二者没有说谁对谁错, 只是基于当前的数据, 作出的合理的判断. 不过由于便捷性和效率, 通常使用 TD 方法, 毕竟 MC 方法太磨叽了.

3.5.3 SARSA: ON-POLICY TD CONTROL

我们也可以直接对 $Q^{\pi}(s,a)$ 进行 TD-Prediction, 该算法也叫 SARSA (State-Action-Reward-State-Action) .

source from refer¹

这个地方 ON-POLICY 是说我们对下一个 action $s_{t+1}$ 的 Q value 预估用的 policy 和获取下一个 action $s_{t+1}$ 的 policy 是同一个.

3.5.4 Q-Learning: Off-Policy TD Control

Q Learning 则是直接类似 3.3.4 节的 Value Iteration. 我们可以直接将 improvement 嵌入到更新公式里边, 直接期望 Q function 收敛到最优的 policy $\pi_{\ast}$ 对应的 Q. 算法如下:

source from refer³

Q-Learning 也被称为 Off-Policy, 是因为我们计算 $r_t + \mathop{\max}\limits_{a} \ Q^{\pi}(s_{t+1},a)$ 的时候用的是 $\mathop{\max}\limits_{a} \ Q^{\pi}(s_{t+1},a)$, 而不是 $\pi$ 真正想输出的 action.

可以这样理解, 存在一个 $\pi_{\ast}$, 使得:

\[\pi_{\ast}(s_{t+1}) = \mathop{\arg\max}\limits_{a} \ Q^{\pi}(s_{t+1},a) \ \text{或者} \ Q^{\pi}(s_{t+1},\pi_{\ast}(s_{t+1})) = \mathop{\max}\limits_{a} \ Q^{\pi}(s_{t+1},a)\]

于是, 每次对下一个 action $s_{t+1}$ 的 Q value 预估的时候, 实际上用的 policy 是 $\pi_{\ast}$, 而基于当前 state $s_t$ 采取 action 的 policy 是 $\pi$. 二者不是同一个, 因此叫 Off-Policy.

这个过程就是”培养” $\pi$, 去尽量向着最优的 $\pi_{\ast}$ 给的方向走.

---

实作上, 由于大家现在都是 neural network 了, 可以直接使用梯度下降去 $\text{minimize}$ 误差:

\[\text{minimize} \ Q^{\pi}(s_i,a_i) \leftrightarrow r_i + \mathop{\arg\max}\limits_{a} \ Q^{\pi}(s_{i+1},a), where \ a = \pi(s_{i+1})\]

算法如下:

[1]. 初始化 Q-function $Q^{\pi}(s,a)$, target Q-function $\tilde{Q^{\pi}}(s,a)$

[2]. 然后对每个 state 都采取 action a, where $a = \mathop{\arg\max}\limits_{a} \ Q^{\pi}(s,a)$

[3]. 这样就能收集到一批 4 元对 : {$s_t,a_t,r_t,s_{t+1}$} 到 buffer 里边(buffer里边的数据要及时更换, 把太早的丢掉, 用更新的 $Q^{\pi}$ 产生的数据放进去.).

[4]. 从 buffer 里边 sample 一笔数据, {$s_i,a_i,r_i,s_{i+1}$}.

[5]. 由于等式左右两边都在变, 考虑到稳定性, 我们用 target Q-function (fixed) 去替换 $\mathop{\arg\max}\limits_{a} \ Q^{\pi}(s_{i+1},a)$, 于是优化目标变为:

\[minimize \ Q^{\pi}(s_i,a_i) \leftrightarrow r_i + \mathop{\arg\max}\limits_{a} \boldsymbol{\tilde{Q^{\pi}}(s_{i+1},a)}\]

上边的式子还有一个问题, 就是后边

\[\mathop{\arg\max}\limits_{a} \ \tilde{Q^{\pi}}(s_{i+1},a)\]

完全是由 Target Net 来选择高分的 action. Double DQN 发现, Target Net 总是高估自己的 action 的分数, 于是提出用 2 个 net 相互制衡, 实作很简单, 直接 action 输出使用正在更新的 $\pi$ 即可, 然后打分还是用 $\tilde{Q^{\pi}}$ :

\[\mathop{\arg\max}\limits_{a} \ \tilde{Q^{\pi}}(s_{i+1},Q^{\pi}(s_{i+1},a))\]

换个更常见的写法, 优化目标最终变为:

\[minimize \ Q^{\pi}(s_i,a_i) \leftrightarrow r_i + \boldsymbol{\tilde{Q^{\pi}}(s_{i+1},\mathop{\arg\max}\limits_{a} Q^{\pi}(s_{i+1},a))}\]

[7]. if step % C = 0, $\tilde{Q^{\pi}} = Q^{\pi}$

这里需要注意的是, $\pi$ 只有一个, 只是 Q function 有 2 个, 其中 $\tilde{Q^{\pi}}$ 的引入只是为了更新的稳定性(如果不考虑稳定性, 那就是原始算法). 但是无论如何, 目标就是要让 $\pi$ 逼近潜在的最优的 $\pi_{\ast}$. (off-policy)

3.5.5 SARSA VS Q-Learning

这里有一个例子, 图中 Cliff 区域的奖励是 -100, 其他区域奖励为 -1. 可以看到 Q-Learning 尽管每次 action 的选取用到了 $\epsilon - greedy$, 但是我们做 Q 值预测的时候, 总是选择 $\text{max}$ 的, 这就导致最后 Q-Learning 收敛到 optimize policy. 而 SARSA 得到则是相对次优的:

source from refer¹

3.5.6 DP VS TD

DP 方法参考 3.3节. 下边给出 DP 和 TD 方法的区别和联系.

3.5.7 Forward View of TD-$\lambda$

前边我们只是向后观察 1 步:

\[Q(s_t,a_t) = Q(s_t,a_t) + \alpha (r_t + \gamma Q(s_{t+1},a_{t+1}) - Q(s_t,a_t))\]

我们可以向后观察 2 步:

\[Q(s_t,a_t) = Q(s_t,a_t) + \alpha (r_t + r_{t+1} + \gamma ^ 2 Q(s_{t+2},a_{t+2}) - Q(s_t,a_t))\]

可以向后观察 k 步:

\[Q(s_t,a_t) = Q(s_t,a_t) + \alpha (r_t + r_{t+1} + ... + r_{t+k-1} + \gamma ^ k Q(s_{t+k},a_{t+k}) - Q(s_t,a_t))\]

上式全部为 $Q(s_t,a_t)$, 我们可以使用加权取平均对所有结果, 记:

\[\begin{align*} G_t^1 &= r_t + \gamma Q(s_{t+1},a_{t+1}) \newline G_t^2 &= r_t + r_{t+1} + \gamma ^ 2 Q(s_{t+2},a_{t+2}) \newline ... \newline G_t^k &= r_t + r_{t+1} + ... + r_{t+k-1} + \gamma ^ k Q(s_{t+k},a_{t+k}) \newline \end{align*}\]

$\lambda$ 加权平均:

\[\begin{align*} G &= \sum^{k \rightarrow \infty} \frac {1}{1 + \lambda + ... + \lambda^{k-1} } (G_t^1 + \lambda G_t^2 + \lambda^2 G_t^3 + ... + \lambda^{k-1} G_t^k) \newline &= (1 - \lambda ) \sum^{k \rightarrow \infty} (G_t^1 + \lambda G_t^2 + \lambda^2 G_t^3 + ... + \lambda^{k-1} G_t^k) \newline &= (1 - \lambda ) \sum^{k \rightarrow \infty} \lambda^{k-1} G_t^k \end{align*}\]

其中, $\frac {1}{1 + \lambda + … + \lambda^{k-1} }$ 使得权重求和为 1.

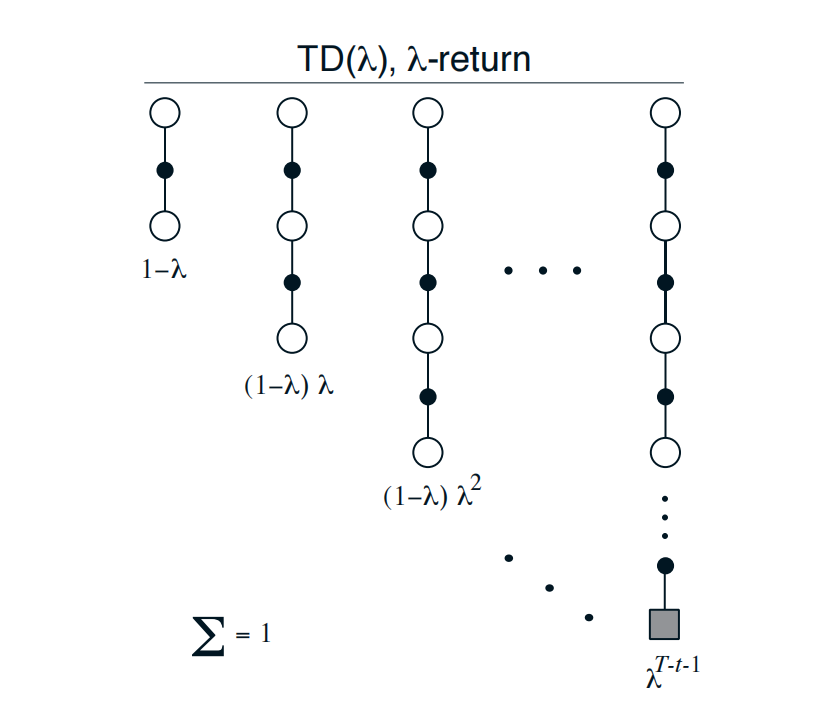source from refer¹

上述版本称为 Forward View of TD(λ). 原因是我们站在当前 time step 向后观察每个 state 的情况, 越往后的 state, 所分配的更新权重越小(对当前的 state $s_t$ 影响越小):

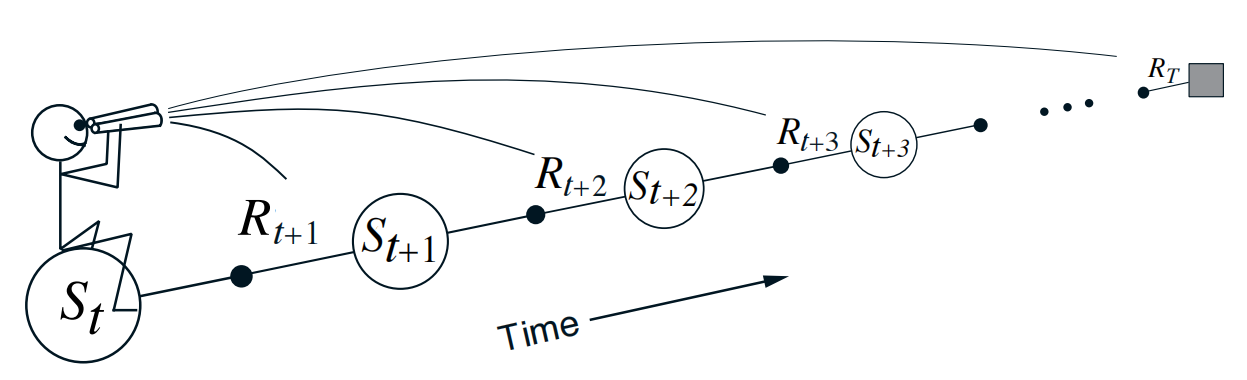source from refer¹

3.5.8 Backward View of TD-$\lambda$

这里需要引入 eligibility trace. 其定义公式如下:

\[E(S) \leftarrow \gamma \lambda E(S) + \mathbb{1}(S = s)\]

上述公式的逻辑是这样的. 假设有一个特定的 state s. 如果当前这轮更新 Q 的时候, 遇到的 state 就是 s, 那么

\[E(s) \leftarrow \gamma \lambda E(s) + 1\]

否则, 就是当前 state 是其他的 $\text{s’}$, 那么

\[E(s) \leftarrow \gamma \lambda E(s)\]

如果一个 state s 经常多次出现, 那么属于这个 s 的 $E(s)$ 就会比较大, 反之就会由于 $\gamma \lambda$ 的存在衰减到 0.

此外 Dutch traces, 当 visit 一个 state 时, 会在之前的基础上先做一个衰减, 然后再加 1. 还有一种是 replacing trace, 当 visit 一个 state 时, 直接会把 traces 置为 1 :

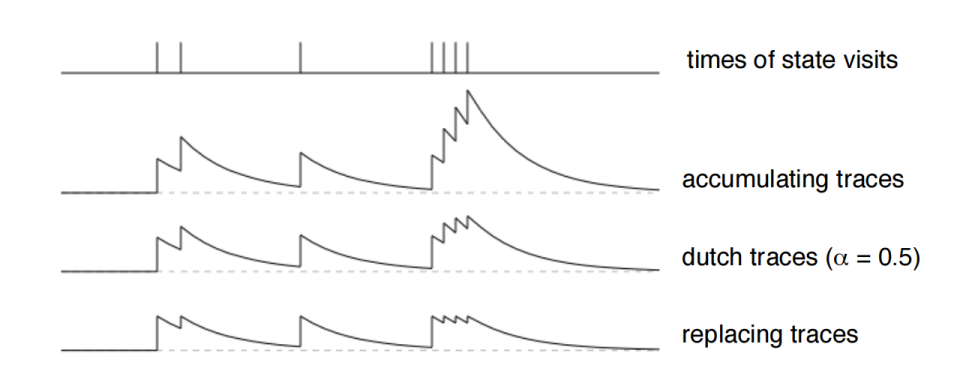source from refer¹

算法过程如下:

source from refer¹

需要注意的是, 虽然当前遇到的 state 是 S, 内部的 for 循环在更新 $V(s)$ 的时候, 都使用同一个 $\delta \leftarrow R + \gamma V(S’) - V(S) $ 对所有的 state 更新.

这个被称为 Backward View of TD-$\lambda$, 是因为我们对每个 sate s 更新的时候, 是基于当前 state S 的 TD-error, 只不过同时还基于 state s 对应的 $E(s)$. 如果 state s 距当前 state S 很远(表现为出现次数很少, 因为我们按时序 visit state), 那么其 $E(s)$ 就会很小, 最后分配的权重就会很小:

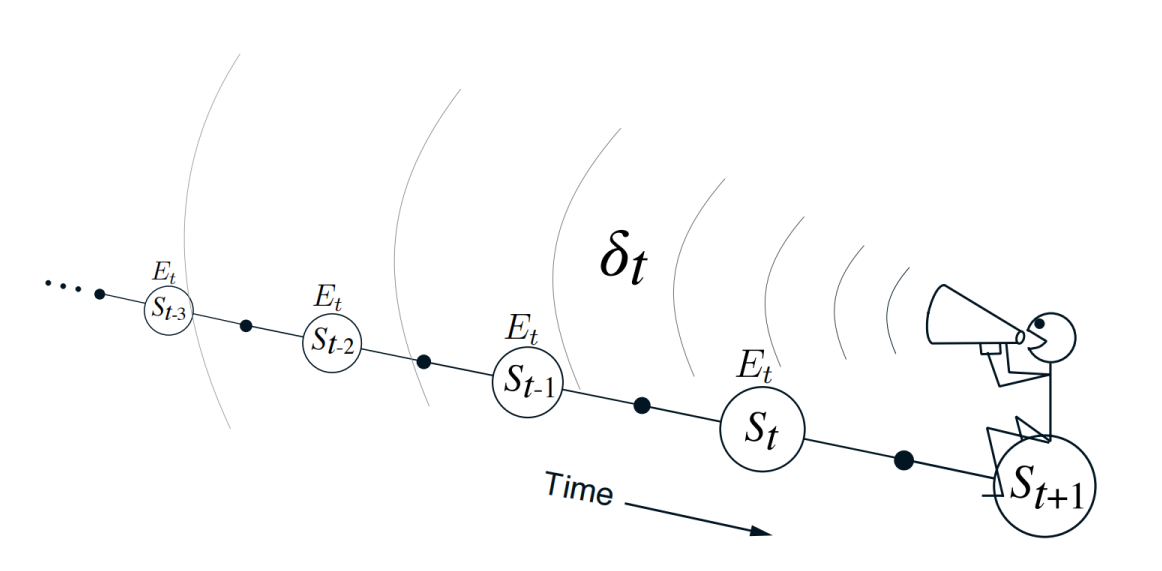source from refer¹

3.5.9 Equivalences of TD-$\lambda$

• $\lambda = 0$

  • forward view

    这个按定义的计算方式, 易知此时就是 TD(0).

  • backward view

    当 $\lambda = 0$ 时, 只有当前 state S 对应的 $E(S) = 1$ , 其他的永远恒为 0. 此时就是 TD(0).

对于 Online(实时更新) 和 Offline(重复收集多个 episode 的数据, 最后进行 batch update) 的学习方式, 由于 $\lambda = 0$ 时, TD(0) 的 reward 计算方式 : $G_t = r_t + \gamma V(s_{t+1})$, 此时的 TD-error 就只关注相邻的 2个 state, 因此最终结果是一样的.

• $\lambda = 1$

  • forward view

    \[\begin{align*} G &= \sum^{k \rightarrow \infty} \frac {1}{1 + \lambda + ... + \lambda^{k-1} } (G_t^1 + \lambda t^2 + \lambda^2 G_t^3 + ... + \lambda^{k-1} G_t^k) \newline &\approx \frac {1}{N } \sum (G_t^1 + G_t^2 + G_t^3 + ... + G_t^N) \ \ (MC 方法) \end{align*}\]

  • backward view

可以看到, 如果看直到 episode 结束的累计错误, 最后再进行 batch update, backward view 的 TD(1) 就是 MC error. 因此, $\lambda = 1 { \& } \ \text{Offinline}$ 时, forward view 和 backward view 是等价的, 均为 MC 方法.

但是, 当进行 Online 更新时, forward view 的 TD(1) 仍然是 MC 方法. 但是 backward view 的 TD(1) 不是了.

• general $\lambda$

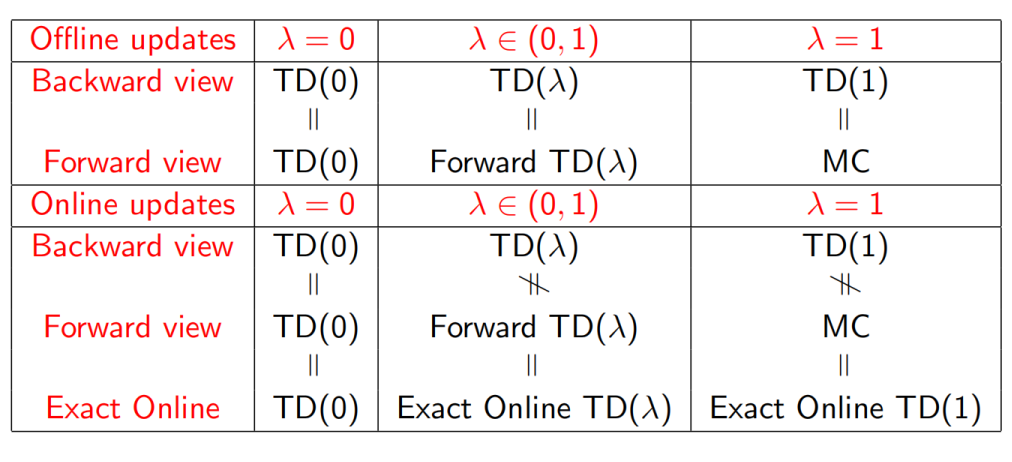
当 $\lambda \in (0,1)$ 结论同理. 同时上述推导过程还显式的证明了在 Offline 的更新方式下, forward view 和 back view 是等价的. 最终给出以下表格:

另外 backward view 和 forward view 的等价证明也可以参考:http://www.incompleteideas.net/book/ebook/node76.html

Reference

1. UCL Course on RL

Footnotes

1. Reinforcement Learning: An Introduction ↩ ↩² ↩³ ↩⁴ ↩⁵ ↩⁶ ↩⁷ ↩⁸ ↩⁹ ↩¹⁰ ↩¹¹ ↩¹² ↩¹³

2. Monte Carlo Methods ↩ ↩²

3. DRL Lecture 3: Q-learning ↩ ↩² ↩³