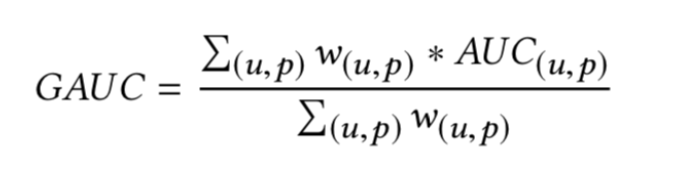AUC & GAUC
0. 前言
AUC 经常被用来评估一个机器学习模型的综合性能, 我们通常听到的版本, AUC 指的是 ROC 曲线下的面积, 不过在实际中他是如何计算的? GAUC 又是什么? 此外, AUC 还有另外一种含义, 描述的是任意取一对儿正负样本, 模型能够把 “正样本” 排序到 “负样本” 前边的能力. 这又是什么?
1. 基本知识
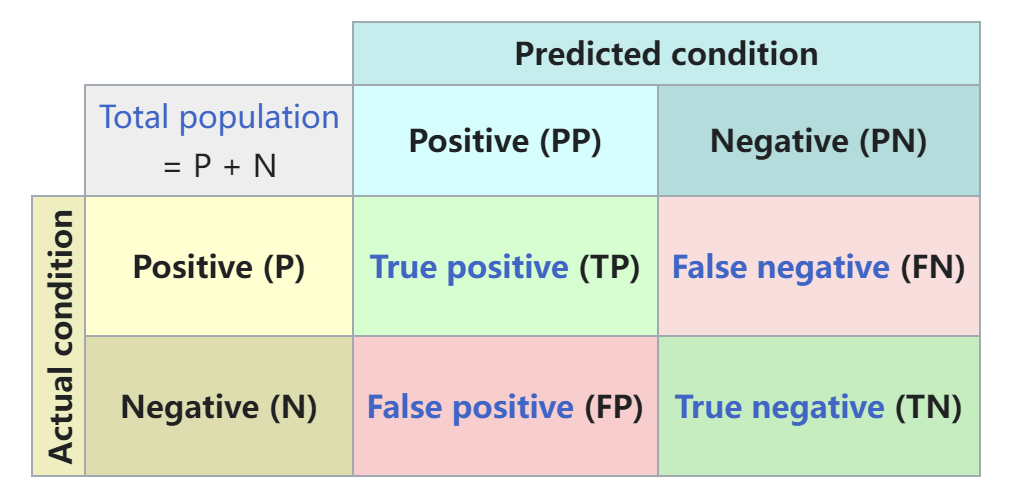
说 AUC 不得不说 ROC (Receiver operating characteristic) 曲线, 说 ROC 曲线又不得不说 混淆矩阵
混淆矩阵用来可视化模型的分类结果, 帮助我们清晰的看到模型在给定某个阈值下对各个类别的覆盖能力如何. 这里简单放个图
绘制ROC曲线主要会用到 2 个指标:
True positive rate (TPR): TPR (真正率), 也叫 Recall (召回), Sensitivity (灵敏度). 它描述的是本身就是正样本, 模型也预测为正样本占所有正样本的比例.
很明显, 阈值越小, TPR 越大, 当阈值为 0, 所有的样本全部预测为正类, 那么 $TPR = 1$ . 反之, 当阈值升高, TPR 下降, 当阈值为 1, 所有的样本全部预测为负类 , 此时 $TPR = 0$
False positive rate (TPR): FPR (假正率). 它描述的是本身就是负样本, 却被模型预测为正样本占所有负样本的比例.
很明显, 阈值越小, FPR 越大, 当阈值为 0, 所有的样本全部预测为正类, 那么 $FPR = 1$ . 反之, 当阈值升高, FPR 下降, 当阈值为 1, 所有的样本全部预测为负类 , 此时 $FPR = 0$ .
可以看到 TPR 和 FPR 的趋势一致. 那么给定一个阈值, 就得到一对儿对应的 TPR 和 FPR , 我们令阈值 从 0 - 1 , 这样就会有很多对儿 TPR 和 FPR . 将其以 FPR 作为横轴, TPR作为纵轴, 就得到了 ROC曲线.
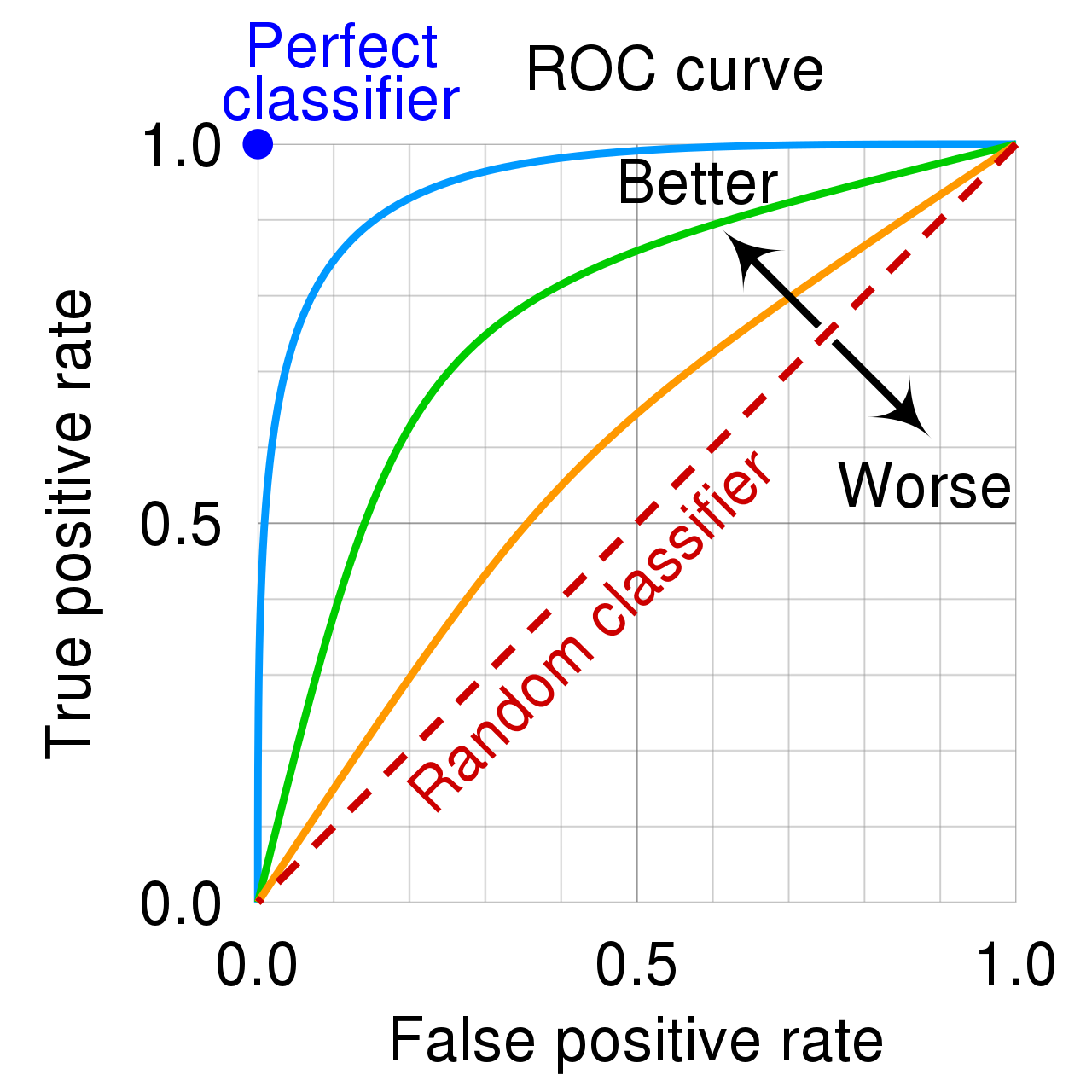
ROC曲线如图 :
[1] ROC 曲线越靠左上方越好, 这表明在给定的阈值下, $TPR > FPR$, 从含义上讲, 就是模型 预测正确的能力(TPR) 比 预测错误的能力(FPR) 要更强.
[2] 中间那条红色的虚线, 表示随机猜测, 此时无论什么阈值, $ TPR == FPR$ , 就是模型 预测正确的能力(TPR) == 预测错误的能力(FPR), 换句话说这个模型没有任何预估能力. 一眼丁真, 鉴定为就是在抛硬币.
2. AUC 的含义
上边说道, ROC 曲线越靠左上方越好, 但是这个可能比较主观, 我们需要用一个定量的指标来描述. 其实 “越靠左上方” 可以用 ROC曲线下的面积(Area Under the Curve, AUC) 来描述, 如果下边面积越大, 就说明 “越靠左上方”, 当然如果面积最大到 1, 那就是完美的分类器. 因为此时对任意的阈值 $TPR == 1$ , 即无论什么阈值, 所有的正样本都能够正确识别, 那就只有一种情况:
下面我们从另外的角度看一下 AUC. 首先回顾 $TPR$ 和 $FPR$.
TPR : 预测为正样本, 且本身是正样本的占所有本身是正样本的比例, 即给一个正样本 $X$, 模型预测为正样本的概率 $P(X)$.
FPR : 预测为正样本, 且本身是负样本的占所有本身是负样本的比例, 即给一个负样本 $Y$, 模型预测为正样本的概率 $P(Y)$.
那对于 ROC 的一个点 (FPR, TPR), 假设 TPR > FPR 时(这是我们希望的), 表明给定任意一对儿 (正, 负) 样本 (X, Y), 模型预测结果 P(X) > P(Y), 即本身为正样本的预测输出值 > 本身为负样本的预测输出值.
再换句话说, 假设利用模型的输出对所有样本进行降序排序, 那么排序后的结果, 本身是正样本能排在本身是负样本的前边(以一定概率). 而AUC,作为ROC曲线下的面积,是在所有决策阈值下的概率积分,从而代表了模型在任意阈值下, 对随机选择的 (正, 负) 样本对的排序能力。
3. AUC的计算
显然通过计算曲线下面积的方式要用到积分, 这个可能比较棘手, 我们可以利用另外一种含义的性质来计算.
3.1 算法1
思想 : 我们想评估 模型对任意一对儿 (正, 负) 样本 (X, Y), 模型预测结果 P(X) > P(Y), 即本身为正样本的预测输出值 > 本身为负样本的预测输出值 的能力(即概率) , 将这个进行拆解: 对每一个 正样本遍历, 观测当前正样本 排在 多少个负样本前边, 然后累计, 最后除以总的可排列组合数, 即可得到 “对随机选择的 (正, 负) 样本对 (X, Y) 的 P(X) > P(Y) 排序能力(即概率).”
举个例子:
| class | label | pre |
|---|---|---|
| A | 0 | 0.1 |
| B | 0 | 0.4 |
| C | 1 | 0.3 |
| D | 1 | 0.8 |
总共 2个正样本, 2个负样本, 共 2 * 2 种排列组合
对于正样本C, 其在 1 个负样本前边.
对于正样本D, 其在 2 个负样本前边.
故该模型的AUC为:
\[AUC = \frac {1 + 2} {4} = 0.75\]如果遇见正负样本输出得分一样的呢?将一样的认为是0.5个
| class | label | pre |
|---|---|---|
| A | 0 | 0.1 |
| B | 0 | 0.4 |
| C | 1 | 0.4 |
| D | 1 | 0.8 |
总共 2个正样本, 2个负样本, 共 2 * 2 种排列组合
对于正样本C, ABC 和 ACB 顺序都可以, 所以理解为在 1.5 个负样本前边.
对于正样本D, 其在 2 个负样本前边.
故该模型的AUC为:
\[AUC = \frac {1.5 + 2} {4} = 0.875\]因为这个算法要遍历正样本, 然后与负样本比较计数, 因此复杂度属于 $O(N^2)$ .
3.2 算法2
既然我们需要衡量模型的排序能力, 那不妨先对样本按照模型预测值排个序, 如下表
假设 $M$ 个正样本, $N$ 个负样本
| class | label | pre | rank |
|---|---|---|---|
| A | 0 | 0.1 | 1 |
| B | 0 | 0.4 | 2 |
| C | 1 | 0.4 | 3 |
| D | 1 | 0.8 | 4 |
根据上表的 $RANK$ 可以很容易知道以下成立:
第 1 个正样本 C 的 $rank = 3$ , C 的前边有 2 个负样本 : (不算自己: $rank - 1 = 2$)
第 2 个正样本 D 的 $rank = 4$ , D 的前边有 2 个负样本 : (不算自己和前一个正样本: $rank - 2 = 2$)
同理, 假设对于第 M 个正样本 E , 其 $rank = K$, 则 E 的前边有 $K - M$ 个负样本 .
这样我们就有简单的计算方式, 去计算每个正样本盖过多少个负样本, 从而 AUC 如下:
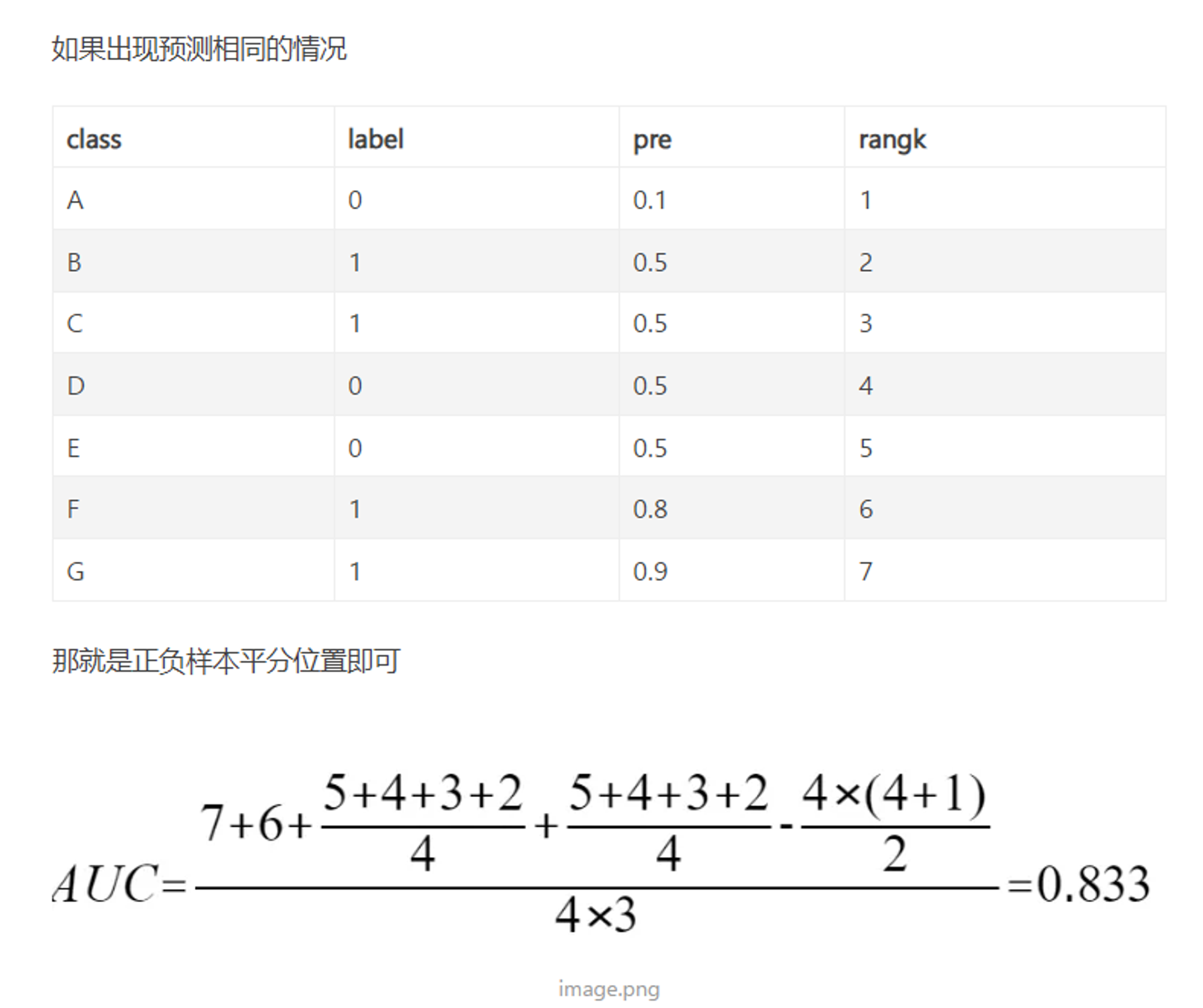
\[\begin{align*} AUC &= \frac {(rank_{x_1} - 1) + (rank_{x_2} - 2) + ... + (rank_{x_M} - M)} {M \times N} \\ &= \frac {(rank_{x_1} + rank_{x_2} + ... + rank_{x_M}) - (1 + 2 + ... + M)} {M \times N} \\ &= \frac {\sum_{i=1}^{M} rank_{x_i} + \frac {M(M+1)} {2}} {M \times N} \end{align*}\]Note : 如果出现预测值相等的情况, 这个时候的 rank 是不确定的, 比如下表结果, 对与 B 样本, 其 $pre = 0.5$ , 和他一样的有 $4$ 个, 这样对于 B 样本, 其可能的 rank 可以是 ${2, 3, 4, 5} $, 所以其实际所发挥的 rank 作用 为 : $\frac {2+3+4+5} {4}$ , 正样本 C 同理 .
4. Group AUC (GAUC) 的含义
AUC 在传统的机器学习二分类中还是很能打的,但是有一种场景,虽然是分类模型,但是却不适用 AUC,即广告推荐领域.
当商品库有多个商品要推荐给你的时候,其实算法并不关心每个商品值得推荐的概率是否够高,具体的业务中,我们只关心要推荐给你的商品的排序是否有效. 即更加关注排序.
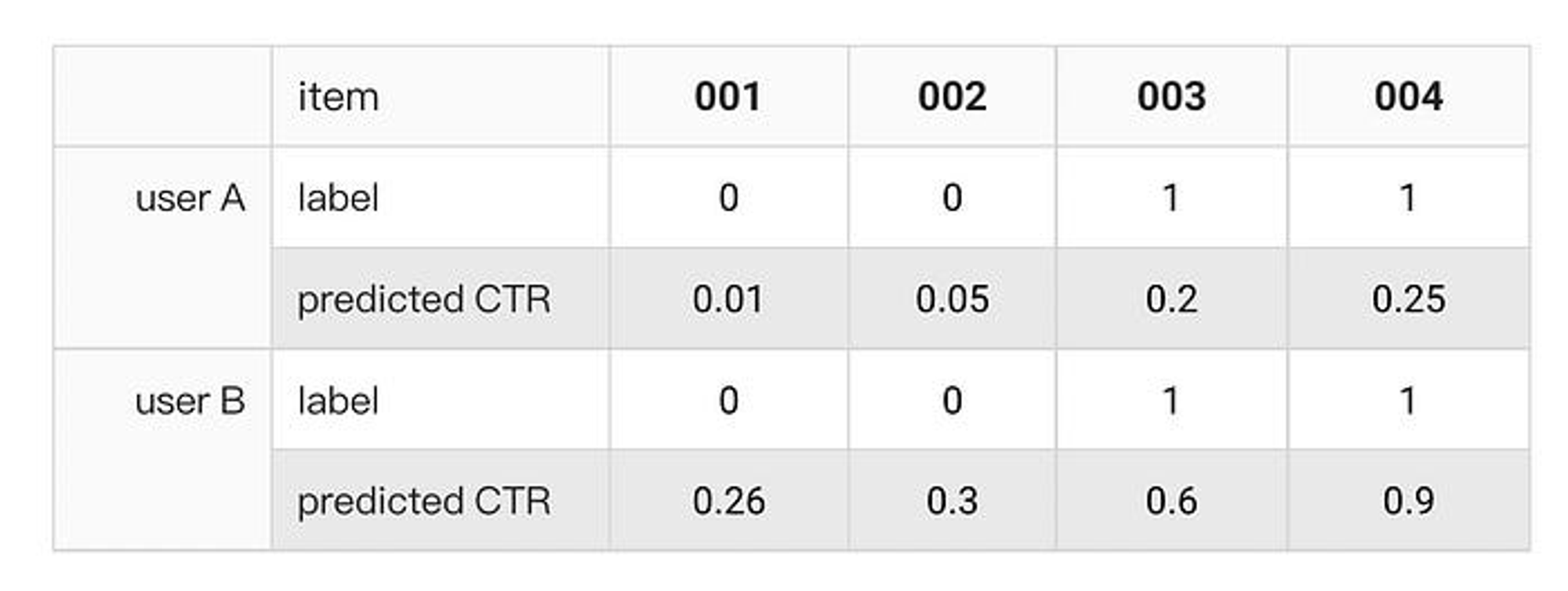
这个时候就有一个问题, 如下表:
对于用户A和B分别来看, 模型对每个item给出的推荐顺序(或者概率)都是符合的 都是可以能够正确分类结果 ( 当然这里可能分类正确与否不是很重要 ), 能够在每个用户身上区分开的 .
每个用户的AUC都是1 , 但是如果把用户A和用户B一起来看, 当成一个用户, 这时候模型对 item 的预测, 给出了不一样的顺序, 这是混合的 AUC = (4 + 4 + 2 + 2) / 16 = 3/4 = 0.75
Group AUC (GAUC) 就是用来解决这个问题, 即通过将不同的用户分组 然后加权计算, 实际中, 权重可以是 不同用户的 click次数 , 基于时间的加权, 基于位置的加权等等.