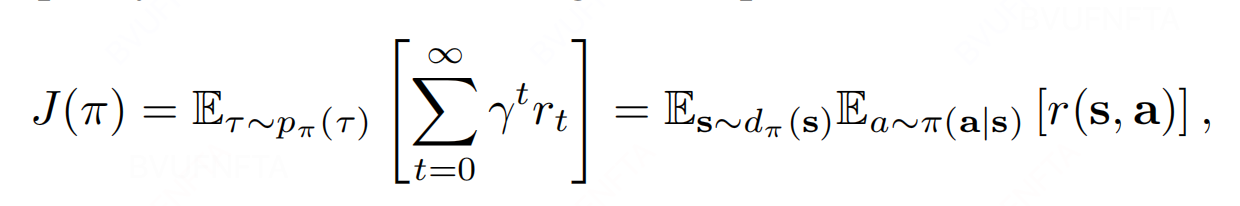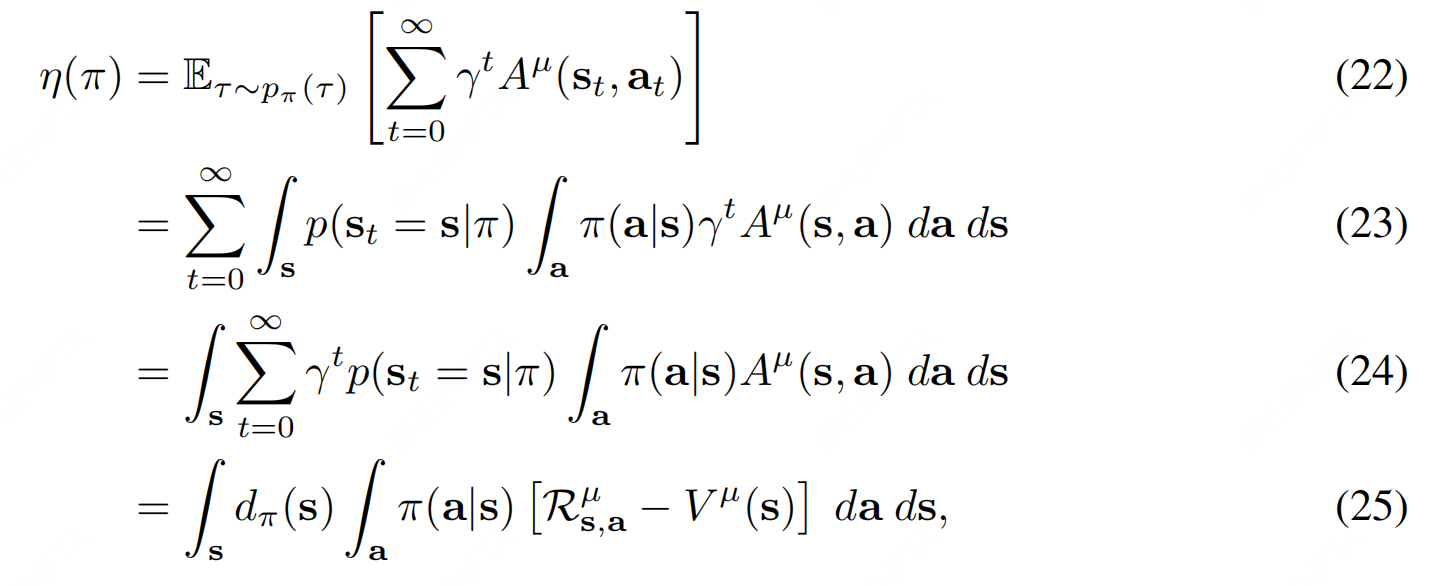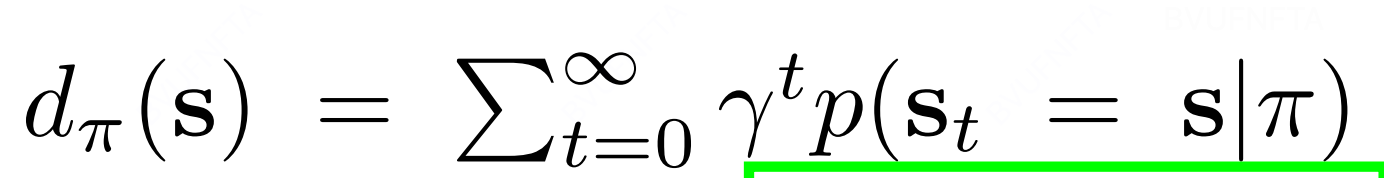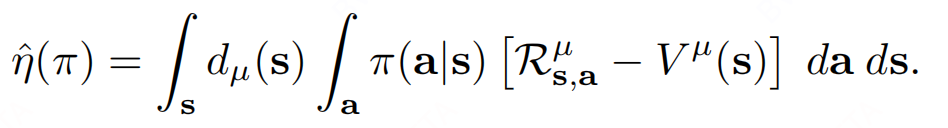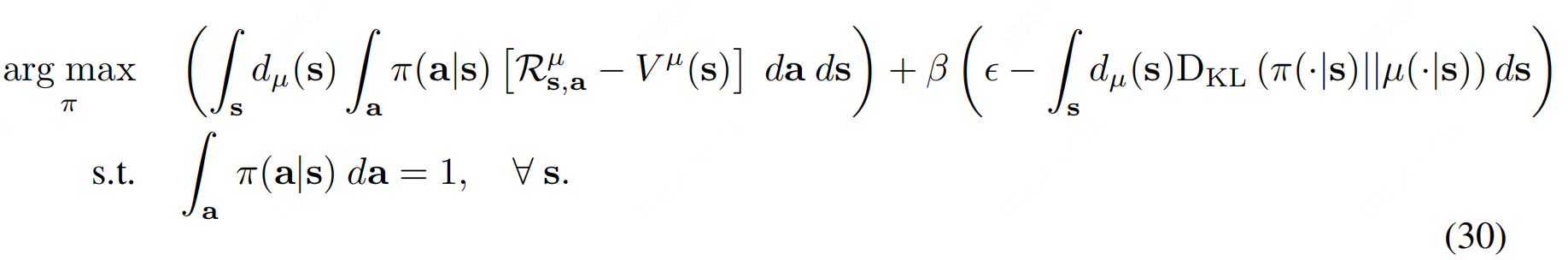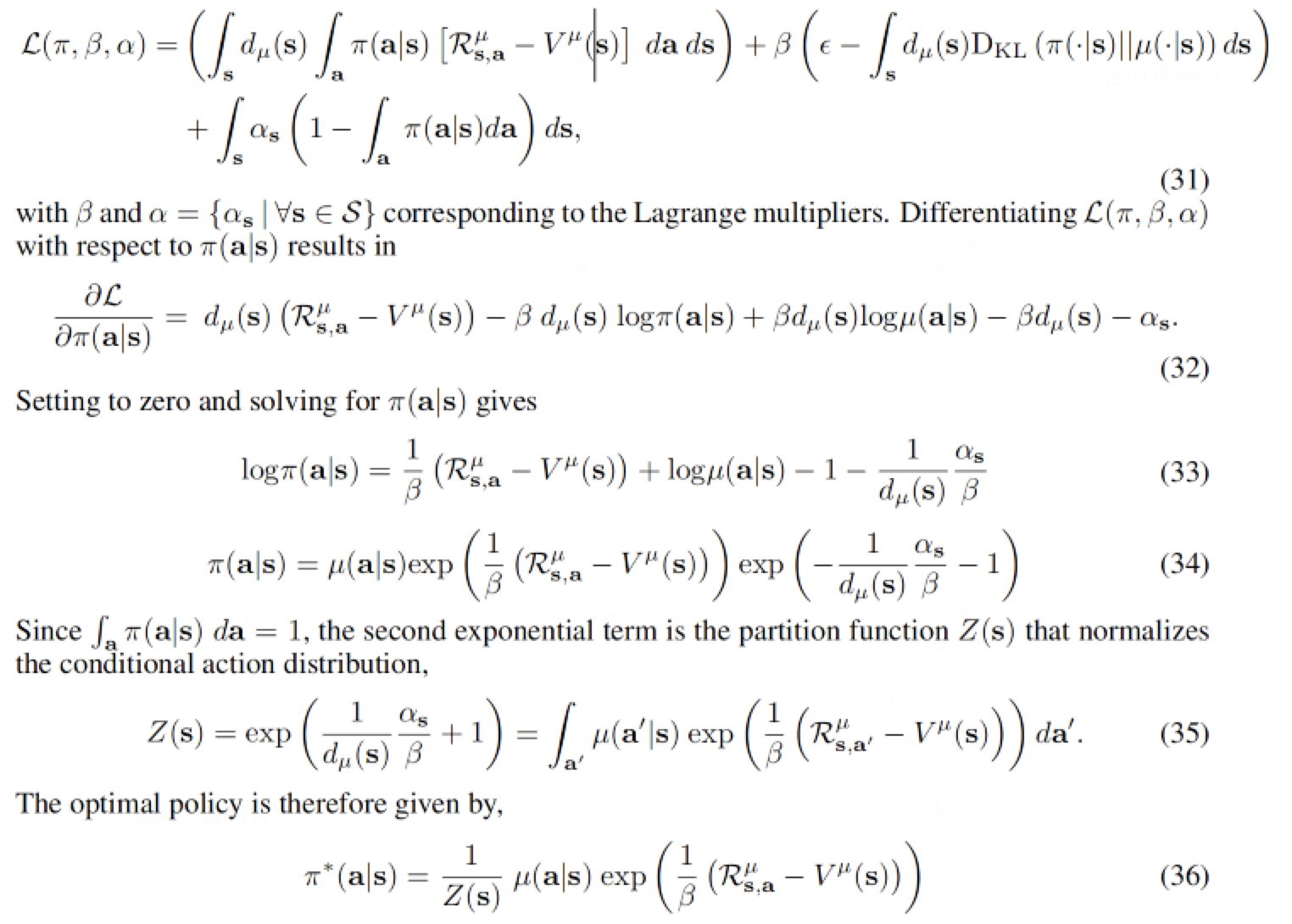A Series on Training LLM Models (I)
0. 前言
本系列主要是对 LLM(Large Language Models) 中涉及到的一些训练方法、技术进行学习.
本篇博客主要对 RLHF(Reinforcement learning from human feedback) 、 PPO (Proximal policy optimization) 、DPO(Direct Preference Optimization) 这 3 个方法以及相应的伪代码进行学习.
内容主要参考 YouTube 上的 Umar Jamil 老师的课程(点击跳转); 老师讲的很不错, 很直观, 建议 follow 学习.
阅读前, 需要你 : 有高数基础知识, 线代基础知识, 统计学习基础知识, 当然还要有 ML和 DL 的知识背景.
1. PPO
PPO(Proximal policy optimization) 这个方法在之前的 blog 中已经有所介绍, 具体可移步至 Deep-Reinforcement-Learning. 以下仅进行简要回顾.
1.1 PPO 目标
首先回顾 PPO 的目标:
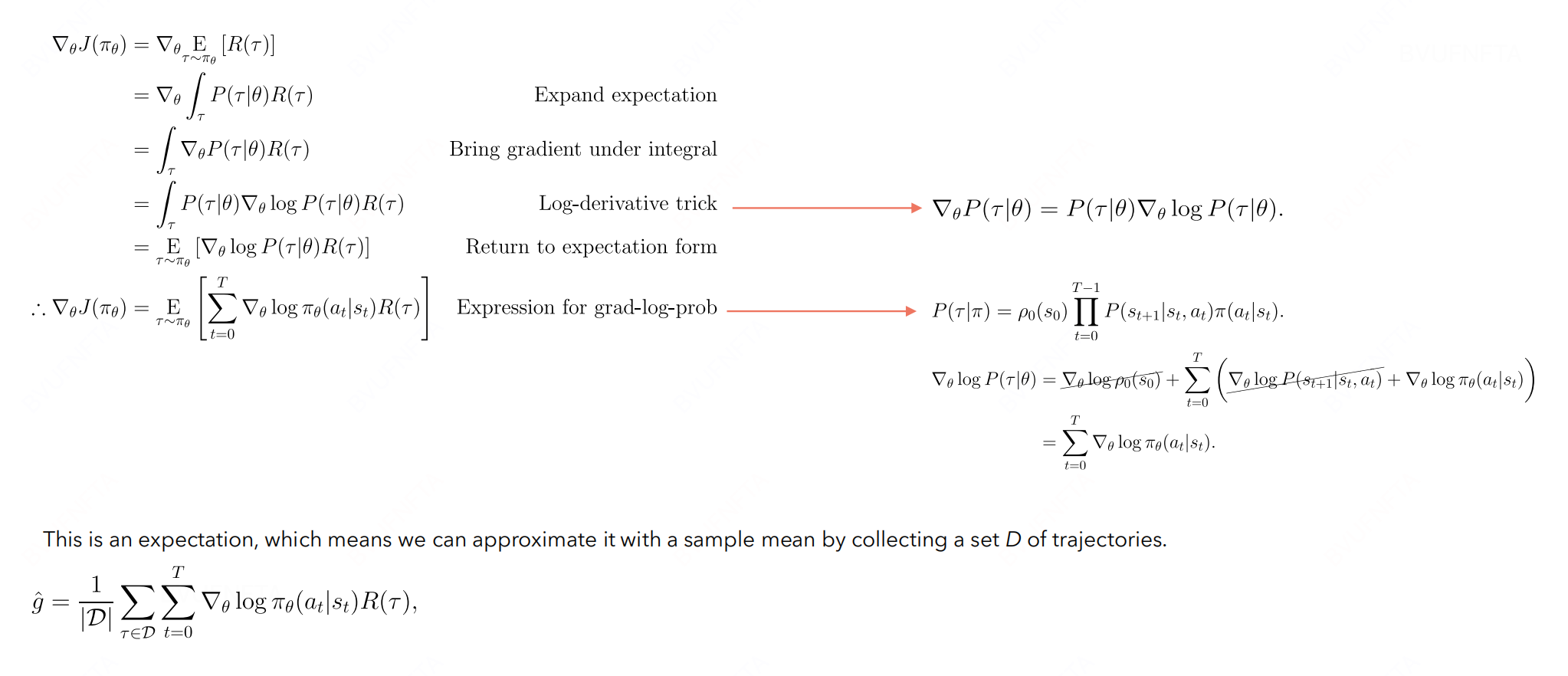
\[max \ \mathbb{E}_{\tau} [R(\tau)] = \sum_{\tau} R(\tau) p(\tau | \theta)\]接着, 计算梯度:
在原始的梯度估计公式中,由于过去的回报与当前动作无关,它们在梯度估计中引入了噪声。这种噪声会导致梯度的方差增加,因为过去的回报对当前动作的梯度更新没有提供有用的信息。
引入“Rewards to go”, 每个时间步的梯度更新只依赖于从当前时间步开始的未来回报。这样做的结果是:
-
减少了无关的噪声(过去的回报)。
-
使梯度估计更加专注于当前动作对未来结果的影响。(即让 model 向更加清晰的梯度方向走)
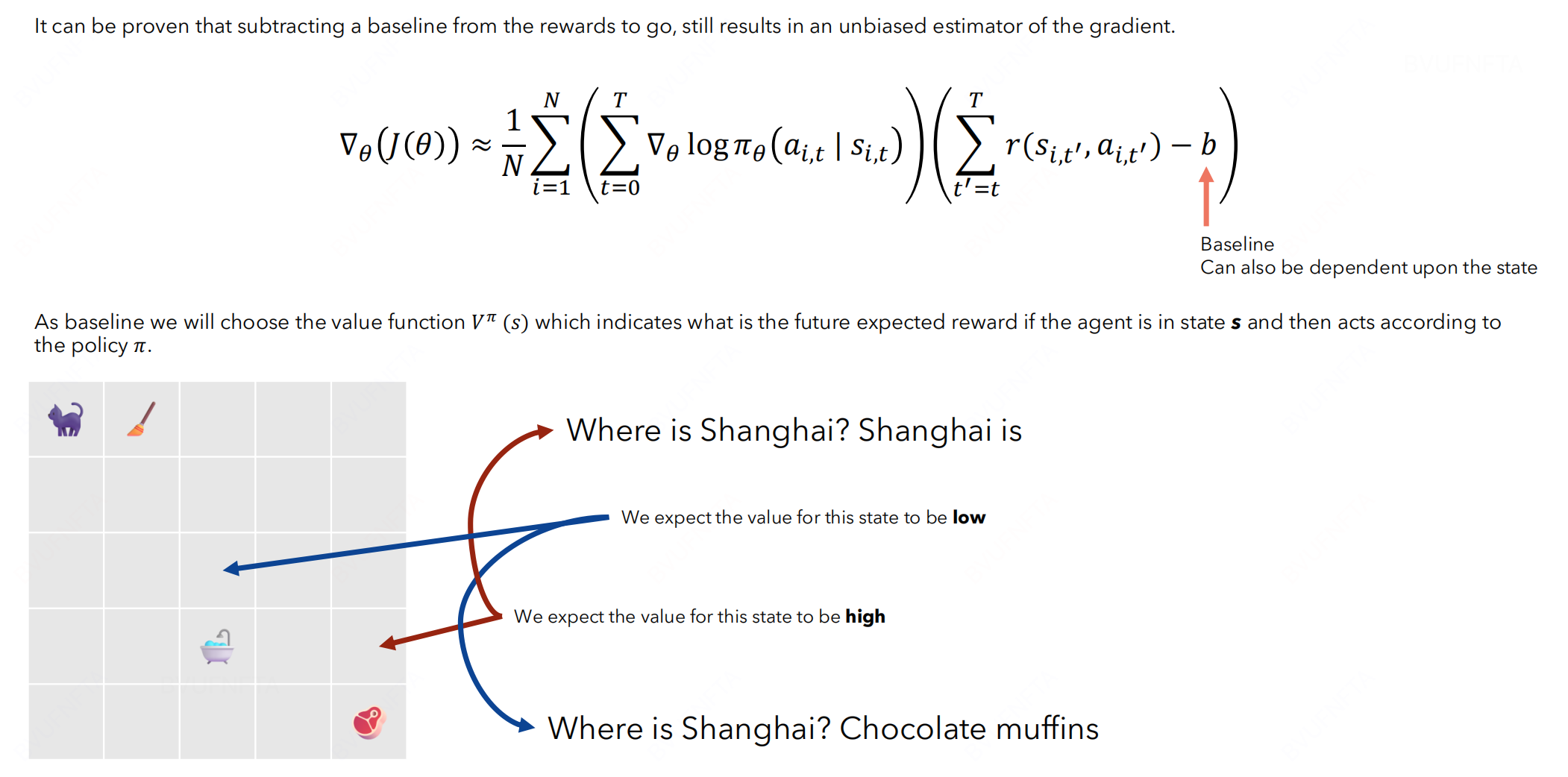
引入 baseline 进一步缓解: 思路是, 找一个 value function 判断当前 state 的情况, 如果不好, 则打一个低分, 反之打高分, 牵引梯度向正确方向, 从而减少 variance.
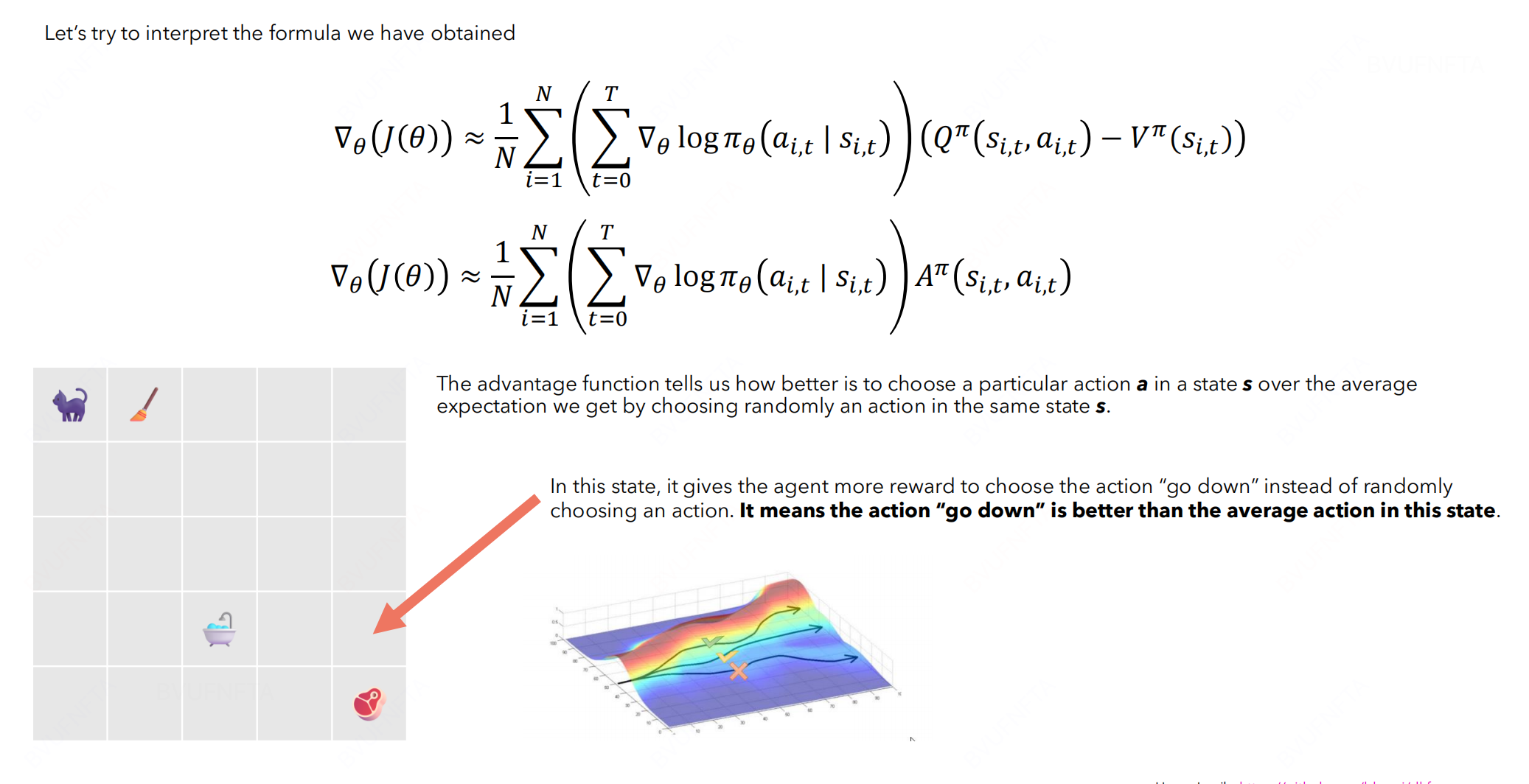
同时, 使用 Q function 代替奖励得分, 可得到如下的表达形式:
1.2 PPO 提效
在计算 advantage term 的时候, 我们可以多向后看几步, 进而能够一定程度减少 bias (因为拿到了更多的真实奖励), 但一定程度上又增加了 variance (因为每次采取action具有不确定性, step越多, 波动性越大).
我们可以对这些 term 进行加权, 得到迭代公式(注意:是反着迭代):
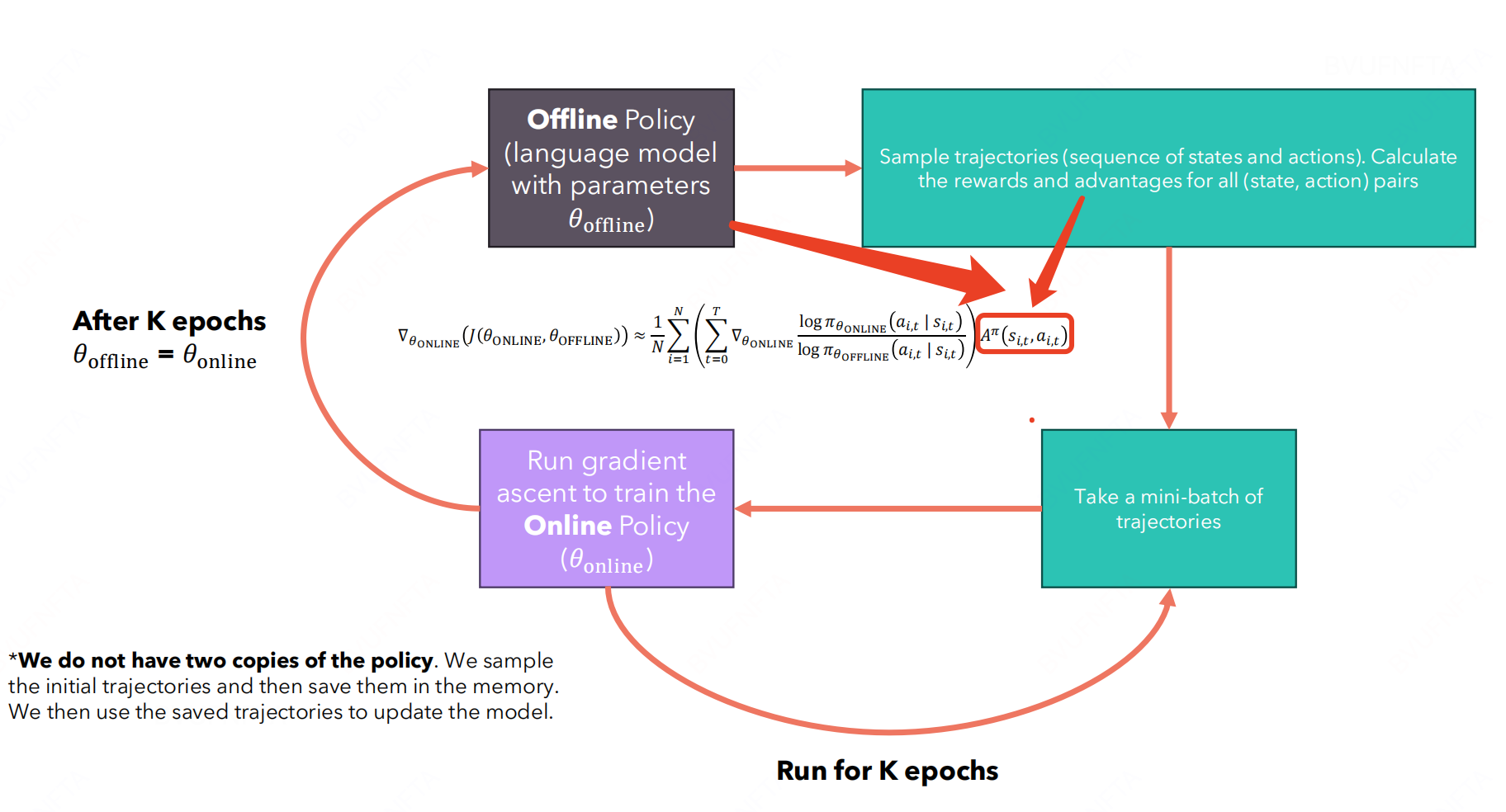
另外, 在计算梯度的时候, 每个 trajectory 只使用了一次(online-policy), 容易造成资源浪费, 因此引入 Importance sampling 和 offline-policy, 如下:
从而得到 PPO 的 loss function:
1.3 Reward 模型训练
由于语言模型的输出, 比较难做到量化打分, 反而容易做比较. 比如 a = “今天的天气真不错” 和 b = “今天的天气挺好的”, 这 2 个句子很难说它们的分数是多少: 75分 or 78分 ? 但是从语感上、拟人化上, 看起来 “今天的天气挺好的” 更加的拟人化一些, 即应该有 R(b) > R(a).
因此, 只需要找一个loss, 能够评估 reward model 的排序能力即可. 二元对比损失(Pairwise Ranking Loss)即满足条件.
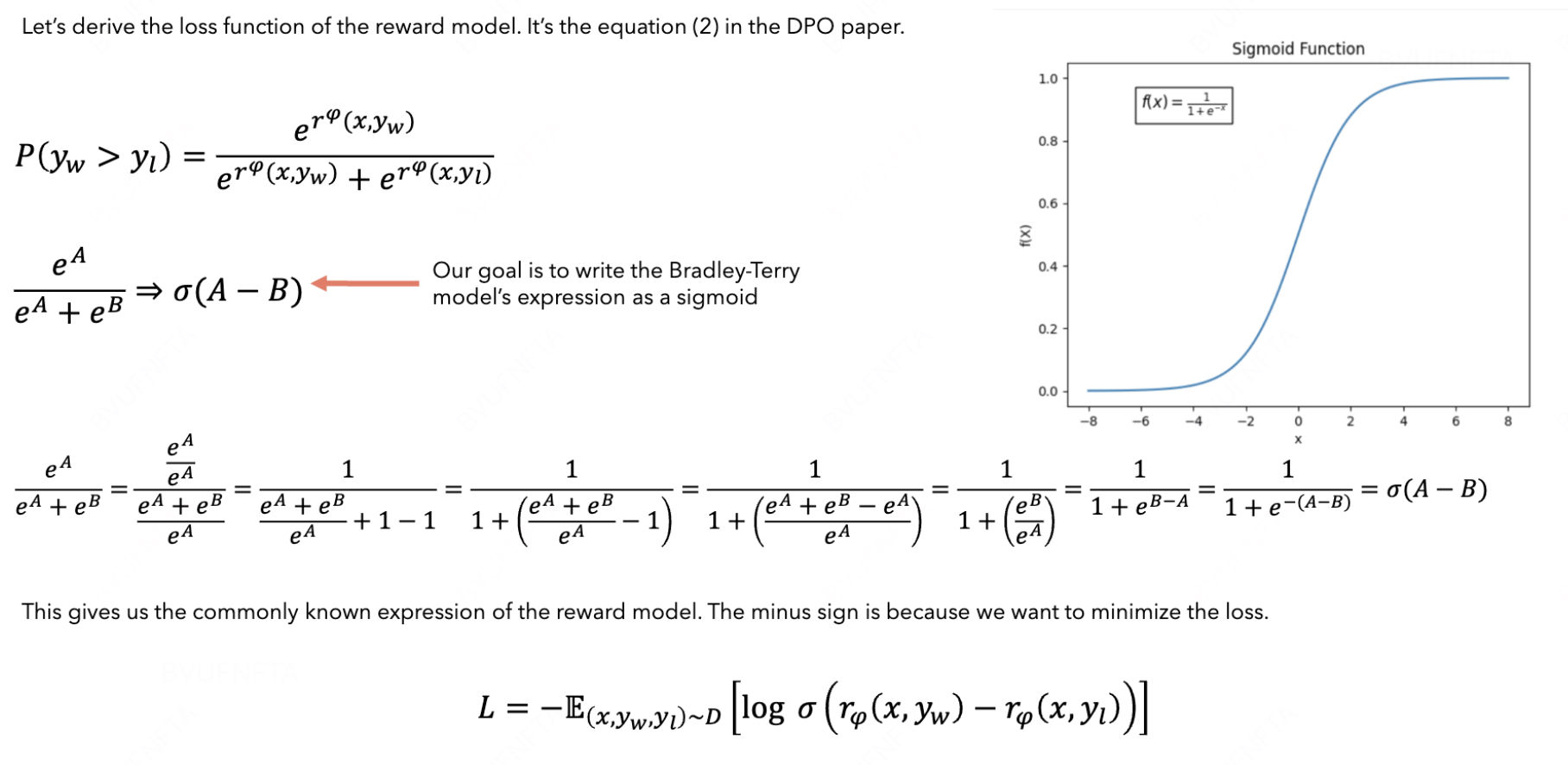
将“优质回答优于劣质回答”的概率 建模为 Bradley-Terry 模型, 然后转换为 loss function 即可:
1.4 怎么实现
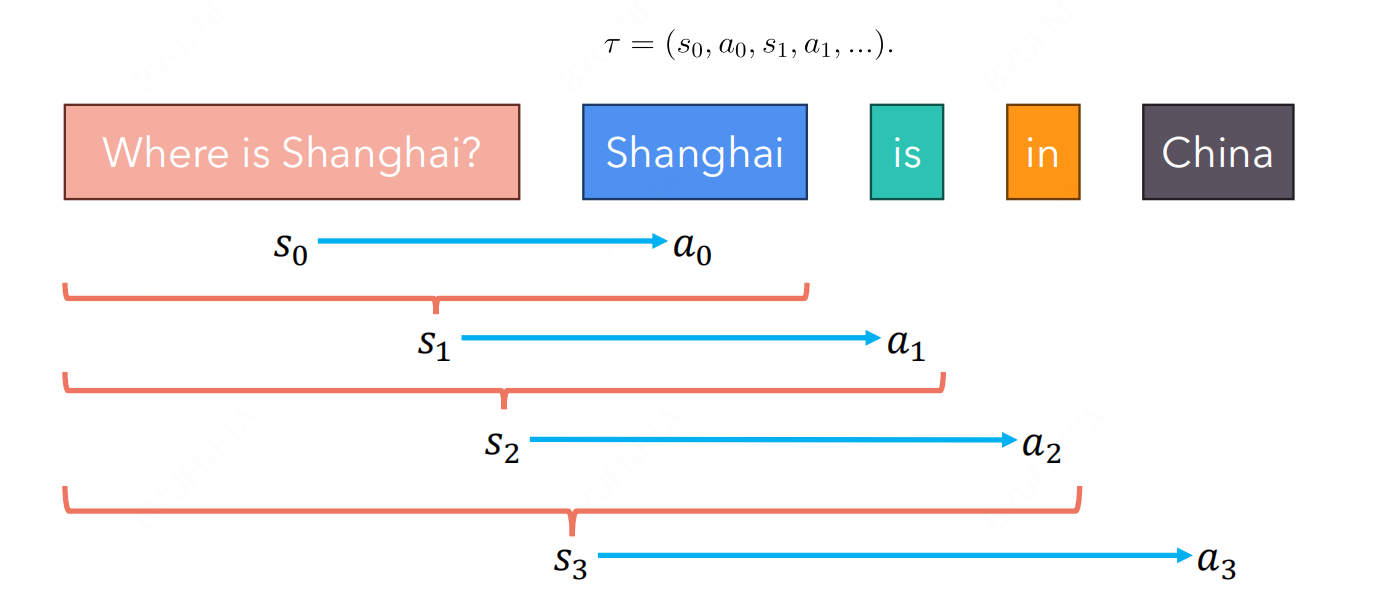
- Trajectory
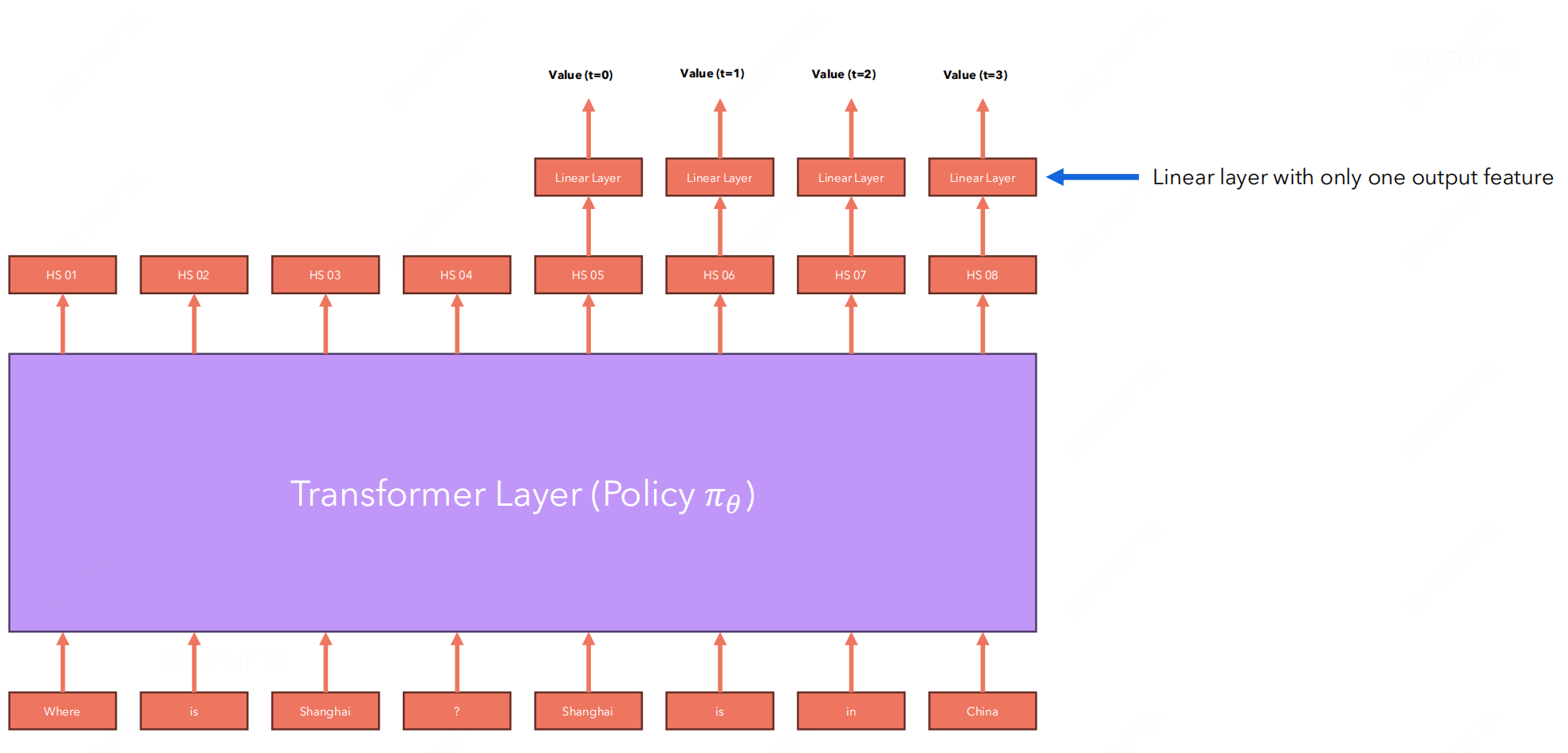
在使用 transformer 模型获取 trajectory 的时候, $(s,a)$ 对儿如下:
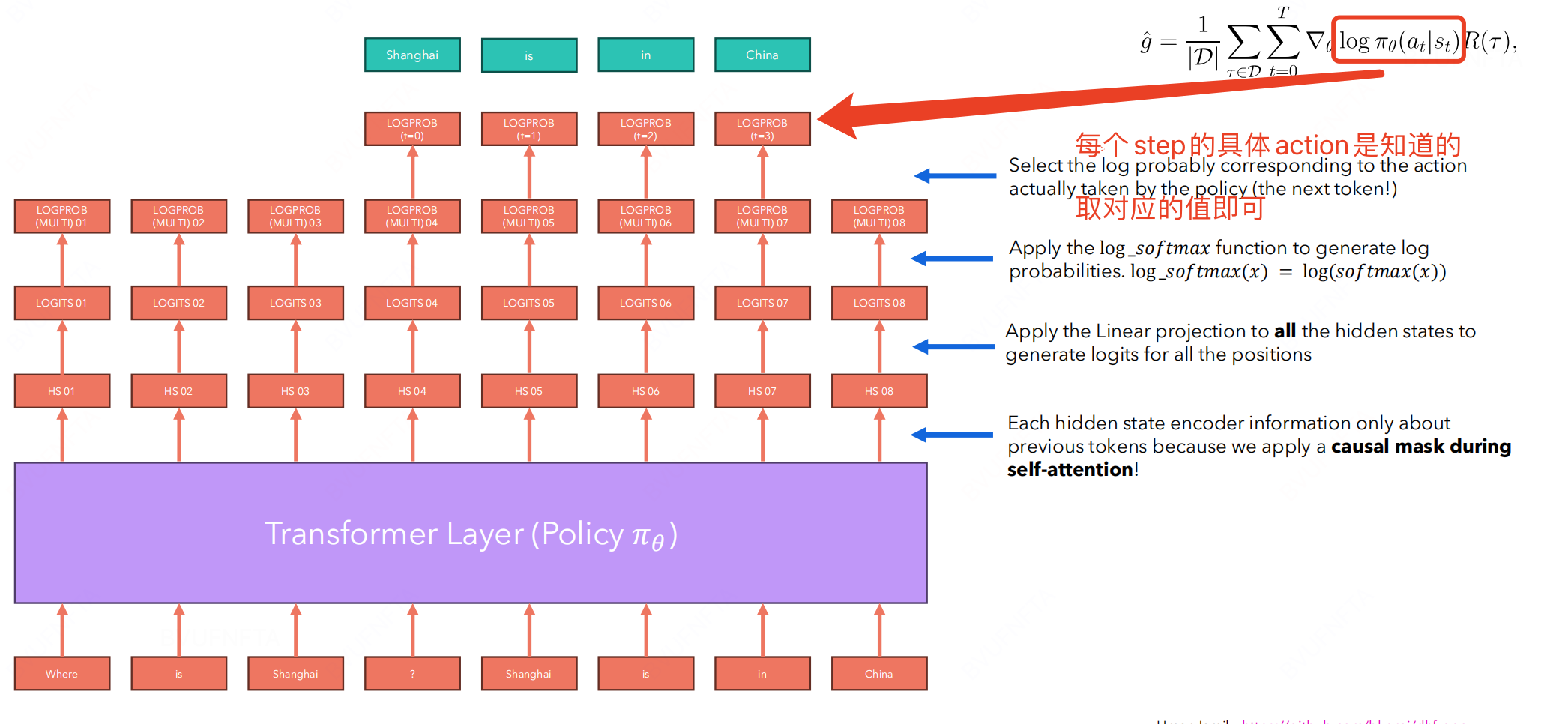
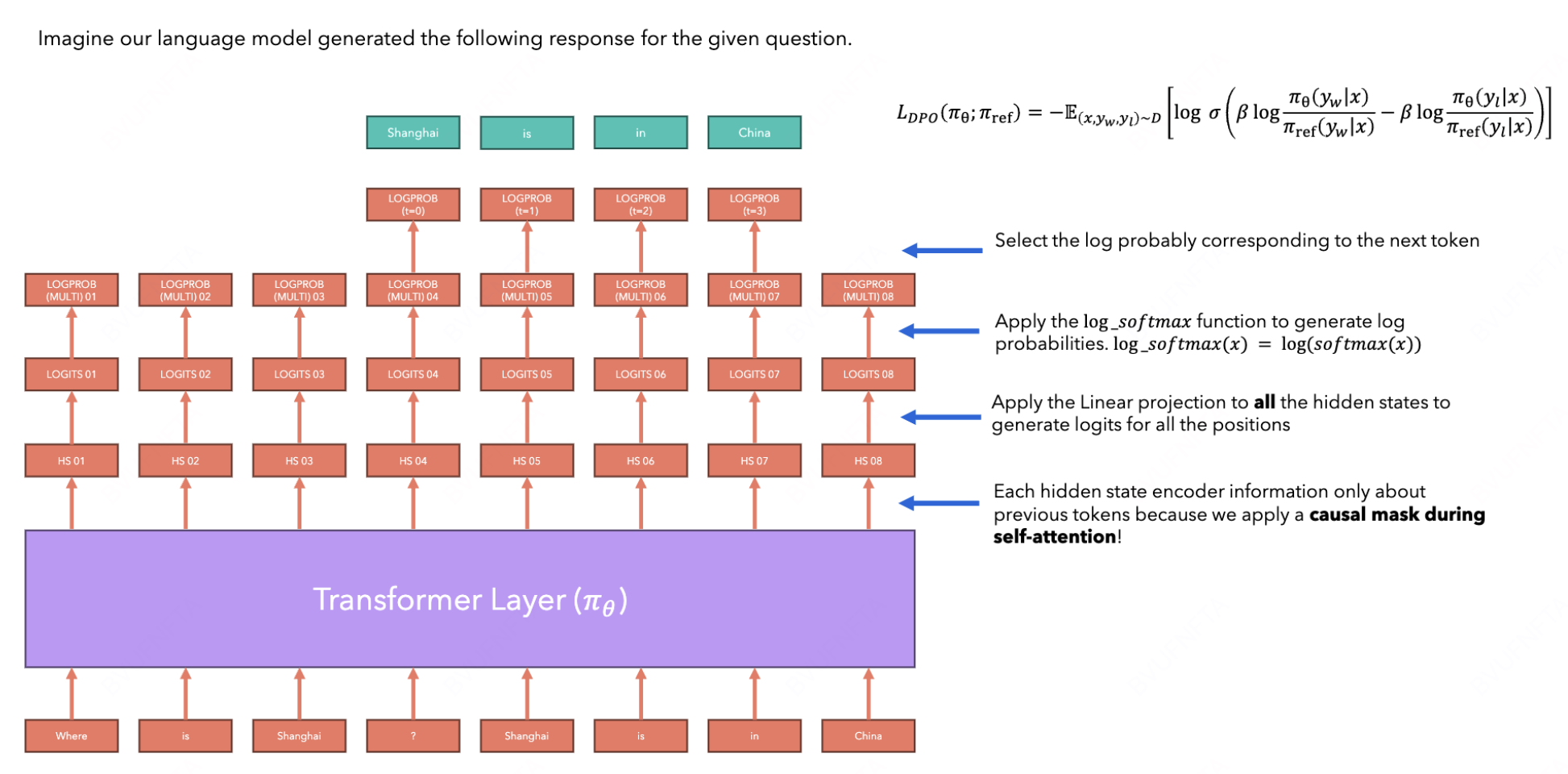
- Log prob of policy
注意: 这里还需要使用 offline-policy 同样计算一次相应的 log probability.
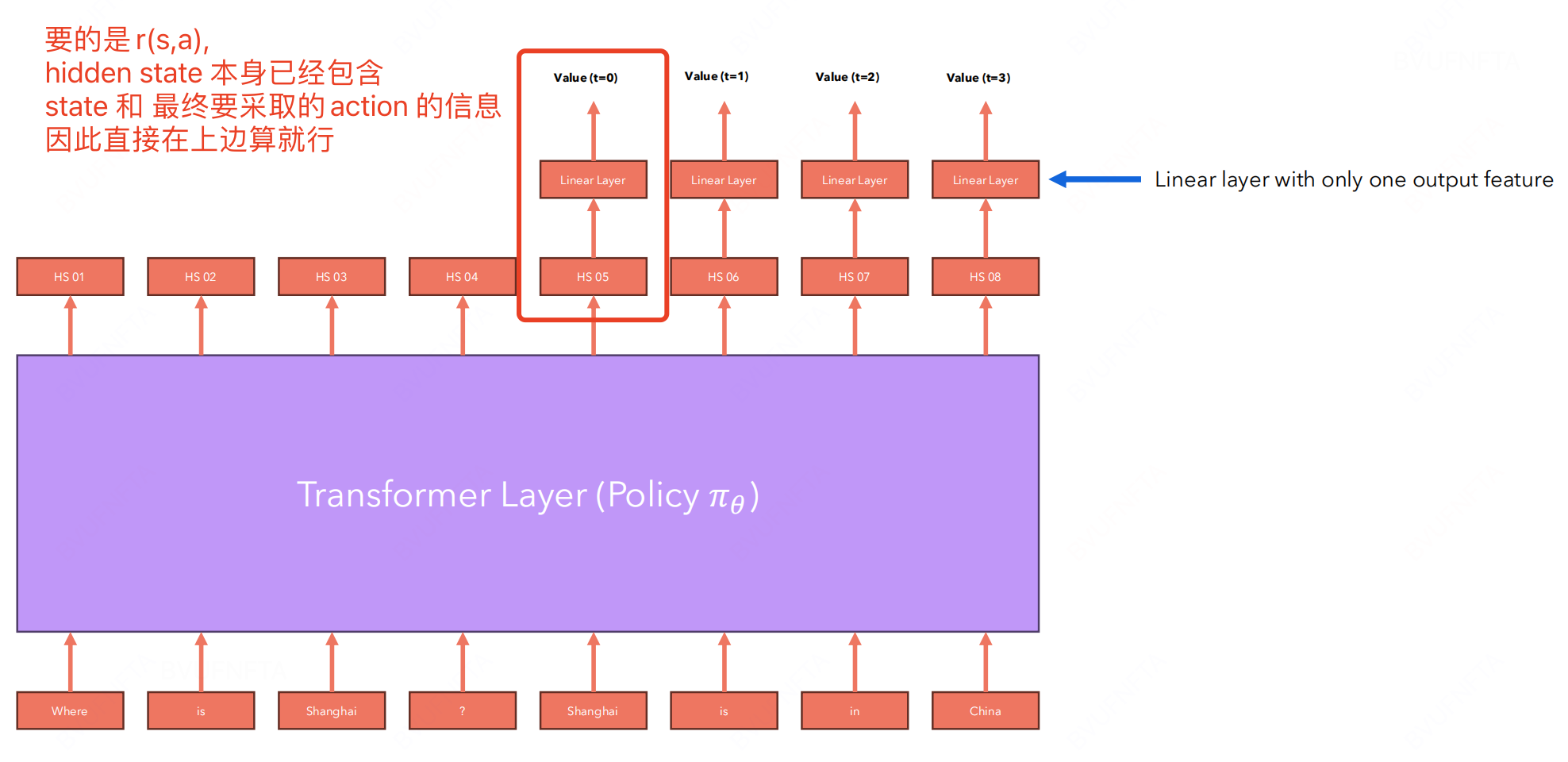
- Reward
直接在 transformer 模型额外加一层输出当前 $(s,a)$ 的 reward:
- V(s)
同理, 额外加一层进行计算即可.
- Advantage term
Advantage term 的计算方式
- Reward Hacking
防止大模型在训练过程中”偷鸡”只输出我们想看的内容(丢失多样性), 可以让训练后的模型和未训练的模型输出计算 KL 散度.
2. RLHF
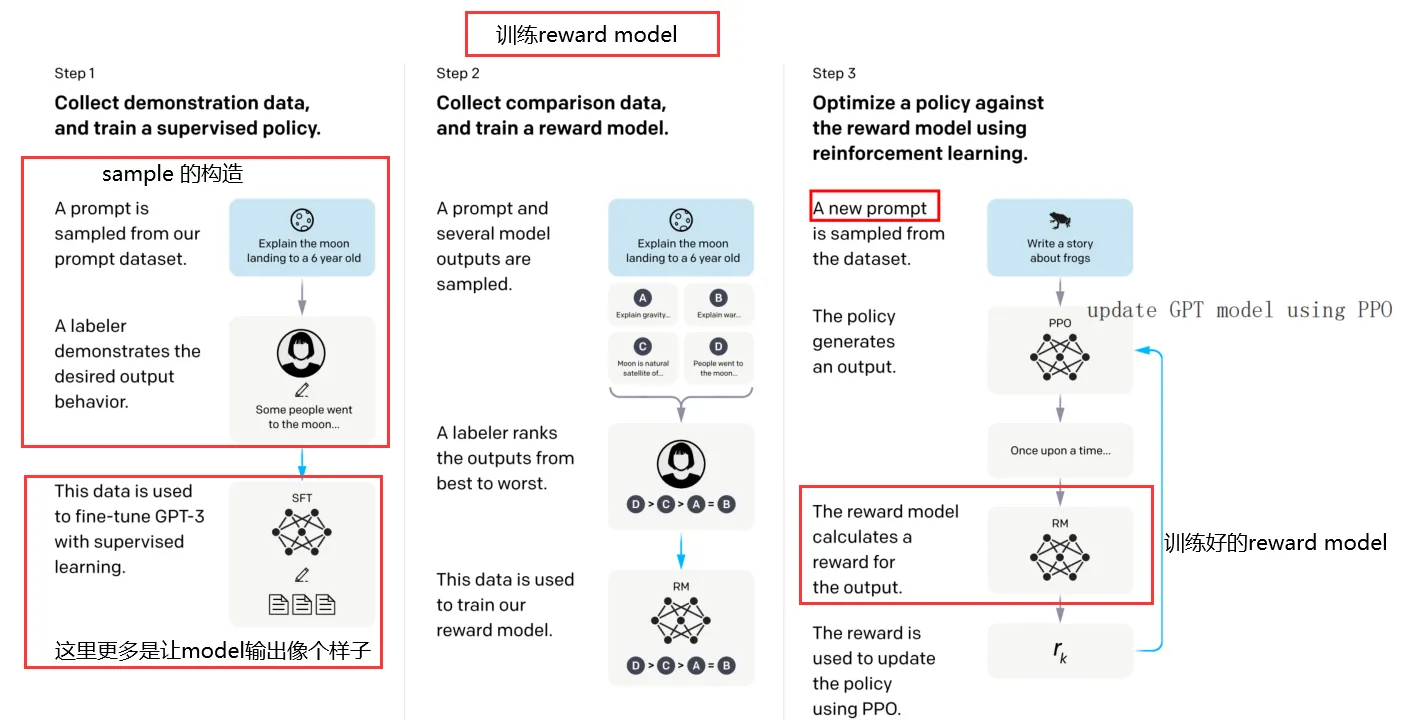
RLHF(Reinforcement learning from human feedback) 可以使用以下图片概括:
- 首先构造 样本输入(比如一些问题、句子的前半句、半句诗等等), 然后招一批 labeler 对这些问题进行解答, 当然也可以直接找网络上的答案, 总之就是给出相应的结果,得到 (input , output)
- 使用上边得到的 (input , output) 对儿, 对 LLM 进行 supervised fine-tune, 使得 LLM 对结果输出像个样子.(起码输出正常的文字, 而不是乱输出标点符号)
- 给一些 prompt, 使用 fine-tuned LLM 产生大量的答案, 然后人工(human feedback) 给这些答案排序 , 然后使用 (prompt, ans1, ans2,..) 训练 Reward model.
- 使用刚刚训练好的 Reward model 结合 PPO 算法对 LLM 进行更新.
3. DPO
3.1 LLM 目标
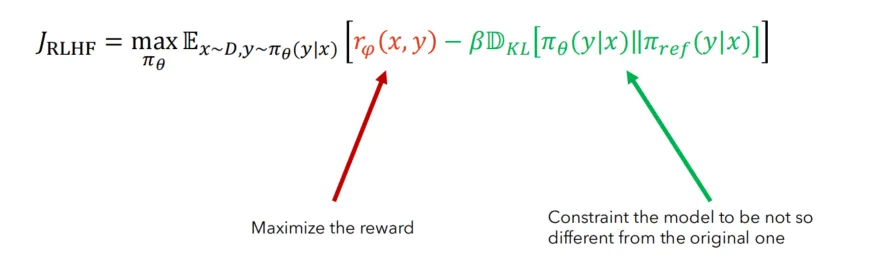
LLM 本质想做的事情, 就是想让输出的结果, 有一个高分而已(假设我们有一个很好的Reward model). 即如下 object
为什么不直接对上边的 $J_{RLHF}$ 进行梯度下降? 因为不能, 上边的输出 $y$ 不是作为一个整体输出的, 而是一个字一个字蹦出来的, 每个字的选择有很多方案, 比如 greddy, beam search ,top-K 等等, 这个 sampling 的过程不是 differentiable 的. 因此只能使用PPO这样的方法: 拆解到每个step, 虽然每个字的选择方案可能不同, 但是这个字的 prob 是已知的, PPO 只需要获取被选择的 prob of step 就能进行优化.
那有没有一种可能, 通过构造一个直接与 Reward 相关的 loss 去优化模型 LLM ? 答案是有的, 我们在 1.3节 训练 Reward 模型时使用的二元对比损失(Pairwise Ranking Loss)就可以帮助我们直接优化 LLM.
因为 reward $r_{\phi}$(x,y) 本身就是把 LLM 的输出 $y$ 放到一个奖励模型中打分, 是与 LLM 的输出有关的. 如果直接用这个损失函数计算梯度, 然后反馈到 LLM 上, 岂不美哉?
3.2 ADVANTAGE-WEIGHTED REGRESSION
问题是怎么把 Reward loss 直接反馈到 LLM 上呢? 首先来看一个方法 advantage-weighted regression 算法. (点击跳转paper)
这个算法给出满足 $max \ J_{RLHF}$ 时, policy $\pi(a_t | s_t)$ 的解析形式(见Paper附录), 这里简要回顾和解释.
Paper首先回顾最原始的目标, 希望训练一个 $\pi$ 能够 $max$ 以下式子:
\[improvement \ \eta(\pi) = J(\pi) - J(\mu) \qquad \qquad (*)\]其中, $\mu$ 是指随机 sampling 一个 policy, $J(\cdot)$ 的定义如下, 最终期望训练得到的 $\pi$ 能够有最大的 improvement reward:
(*)式可以得到如下等价表达方式, 从而转换为我们常见的 RL 表达形式:
此外, 上述表达形式还可以写作如下等价形式:
其中, $ d_{\pi}(s) $ 表达式如下:
但是 $ d_{\pi}(s) $ 和 ${\pi}(s)$ 耦合, 并且 ${\pi}(s)$ 在实时更新, 因此直接优化式(25)比较困难, 但是 $ d_{\mu}(s) $ 是固定的, 因此做一个替代优化:
进而得到以下 constrained policy search problem:
由于, 式(28)是所有的state下, 因此考虑替换为期望 + 软约束(with coefficient $\beta $) :
使用 Lagrange multipliers 法求解 :
3.3 DPO 求解
$J_{RLHF}$ 的格式和式(30)的区别就是把 $R_{s,a}^{\mu} - V^{\mu}(s)$ 换成 $r_{\phi}(x,y)$ , 于是相应的解析解形式为:
现在应该怎么做? 回想 3.1 节的内容(点击跳转), 现在是时候往二元对比损失(Pairwise Ranking Loss)上靠了:
Note: DPO 是跳过 “训练奖励模型” 这个 step , 但是仍然需要人工首先收集一批 label 进行前置性的排序.